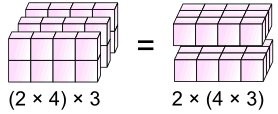交换、结合和分配律
哈!拗口!但其实理念是简单的。
交换律
"交换律"说:我们可以把数的位置对换而答案不变……适用于
…… 加法:
a + b = b + a
例子:
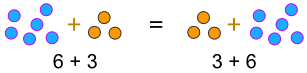
……或 乘法:
a × b = b × a
例子:
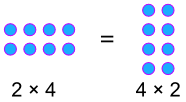

为什么叫"交换"……?
因为数可以对换位置,就像交换礼物一样。
结合律
"结合律"说: 不论我们怎样结合数字(即先计算那些数字),答案都是一样的……适用于
……加法:
(a + b) + c = a + (b + c)
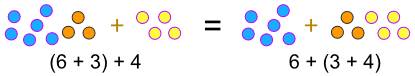
... 或 乘法:
(a × b) × c = a × (b × c)
例子:
| 这个: | (2 + 4) + 5 = 6 + 5 = 11 |
| 与这个的答案是相同的: | 2 + (4 + 5) = 2 + 9 = 11 |
| 这个: | (3 × 4) × 5 = 12 × 5 = 60 |
| 与这个的答案是相同的: | 3 × (4 × 5) = 3 × 20 = 60 |
用途:
有时候用不同的次序去加或乘会比较容易:
19 + 36 + 4 是什么?
19 + 36 + 4 = 19 + (36 + 4) = 19 + 40 = 59
或重新排列一下:
2 × 16 × 5 是什么?
2 × 16 × 5 = (2 × 5) × 16 = 10 × 16 = 160
分配律
"分配律"是最棒的,但你需要小心。
它允许我们:
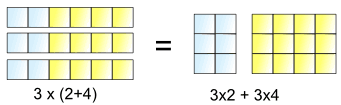
3 份 (2+4) 和 3 份 2 加 3 份 4 是一样的
所以,3× 可以被 "分配" 进 2+4里,变成 3×2 和 3×4
我们这样写:
a × (b + c) = a × b + a × c
自己来计算:
- 3 × (2 + 4) = 3 × 6 = 18
- 3×2 + 3×4 = 6 + 12 = 18
两个方法算出来的答案是相同的。
我们这样说:
以下两个方法的答案是相同的:
- 把一个数乘以一组数的和或
- 把每个乘数分开来做,然后把结果加起来
用途:
有时候把困难的乘数拆开会比较容易:
例子: 6 × 204 是什么?
6 × 204 = 6×200 + 6×4 = 1,200 + 24 = 1,224
或整合:
例子: 16 × 6 + 16 × 4 是什么?
16 × 6 + 16 × 4 = 16 × (6+4) = 16 × 10 = 160
也可以用来做减法:
例子: 26×3 − 24×3
也可以用来做一长串的加数:
例子: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
6×7 + 2×7 + 3×7 + 5×7 + 4×7 = (6+2+3+5+4) × 7 = 20 × 7 = 140
定律就是这样……
……但不要盲目地用!
交换律不适用于减或除:
例子:
- 12 / 3 = 4,但
- 3 / 12 = ¼
结合律不适用于减或除:
例子:
- (9 – 4) – 3 = 5 – 3 = 2,但
- 9 – (4 – 3) = 9 – 1 = 8
分配律不适用于除:
例子:
- 24 / (4 + 8) = 24 / 12 = 2,但
- 24 / 4 + 24 / 8 = 6 + 3 = 9
概要
| 交换律: | a + b = b + a a × b = b × a |
| 结合律: | (a + b) + c = a + (b + c)) (a × b) × c = a × (b × c) |
| 分配律: | a × (b + c) = a × b + a × c |