积分近似值

积分面积

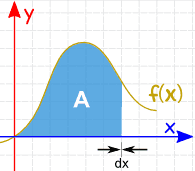
积分是求曲线与轴之间的面积的最好方法：它可以给我们绝对精确答案的公式。

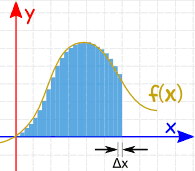
积分面积小delta x

可是，求积分有时是很困难的，甚至可以是不可能计算的！

但我们可以把很多薄片的面积相加
来得到一个近似值。

我们来试试看！

例子！

我们用 f(x) = ln(x)，从 x = 1 到 x = 4

我们其实可以求这个函数的积分，答案是 2.54517744447956……

但假设我们不可以积分，而只能求 ln(x) 的值：

当 x=1：ln(1) = 0
当t x=2：ln(2) = 0.693147……
等等

我们先用宽度为1 的片，这样会解释会容易点（但其实片越薄越好）。

前 4 个方法也称为黎曼和，源自数学家波恩哈德·黎曼。

左矩形法

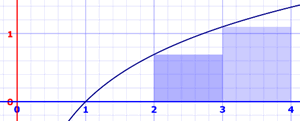
积分近似值左矩形图

这方法用以左边的值为高度的矩形。面积是：

x=1 到 2： ln(1) × 1 = 0 × 1 = 0
x=2 到 3： ln(2) × 1 = 0.693147…… × 1 = 0.693147……
x=3 到 4： ln(3) × 1 = 1.098612…… × 1 = 1.098612……

加起来是 1.791759，比 2.545177小很多。为什么？

因为我们忽略了矩形顶部与曲线之间的面积。

当曲线持续增大时，误差也会越来越大。若曲线有时上升，有时下降，误差通常会比较小。

右矩形法

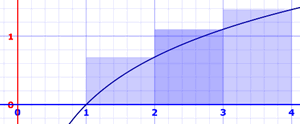
积分近似值右矩形图

在这里，矩形的高度是右边的值。面积是：

x=1 到 2: ln(2) × 1 = 0.693147…… × 1 = 0.693147……
x=2 到 3: ln(3) × 1 = 1.098612…… × 1 = 1.098612……
x=3 到 4: ln(4) × 1 = 1.386294…… × 1 = 1.386294……

加起来是 3.178054，现在比 2.545177 大多了，因为我们也算了矩形顶部与曲线之间的面积。

中点矩形法

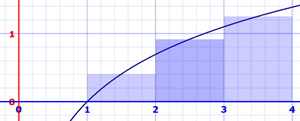
积分近似值中点矩形图

我们也可以用中点！面积是：

x=1 to 2: ln(1.5) × 1 = 0.405465…… × 1 = 0.405465……
x=2 to 3: ln(2.5) × 1 = 0.916291…… × 1 = 0.916291……
x=3 to 4: ln(3.5) × 1 = 1.252763…… × 1 = 1.252763……

加起来是 2.574519……，离 2.545177 很近。

梯形法

积分近似值：梯形法

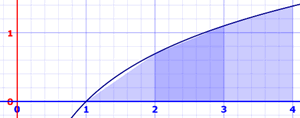
我们可以左右两边都用，这样图形便是个梯形。

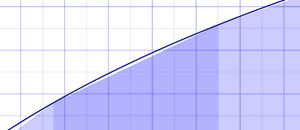
积分近似值：梯形法放大

我们取左边和右边的平均值。面积是：

x=1 到 2: ln(1) + ln(2) 2 × 1 = 0 + 0.693147……2 × 1 = 0.346573……
x=2 到 3: ln(2) + ln(3)2 × 1 = 0.693147…… + 1.098612……2 × 1 = 0.895879……
x=3 到 4: ln(3) + ln(4)2 × 1 = 1.098612…… + 1.386294……2 × 1 = 1.242453……

加起来是 2.484907，还是比 2.545177 小，主要是因为曲线在这个区间是下凹的。

注意每个值用了两次（头尾除外），然后总和被除以 2：

ln(1) + ln(2) 2 × 1 + ln(2) + ln(3) 2 × 1 + ln(3) + ln(4) 2 × 1

1 2 × ( ln(1) + ln(2) + ln(2) + ln(3) + ln(3) + ln(4) )

1 2 × ( ln(1) + 2 ln(2) + 2 ln(3) + ln(4) )

我们可以导出一个通用的公式：

Δx 2 × ( f(x₀) + 2f(x₁) + 2f(x₂) + ... 2f(x_n-1) + f(x_n) )

顺便说，这个方法只不过是左矩形法和右矩形法的平均值：

梯形法 = 左矩形法 + 右矩形法 2

辛普森公式

积分近似值：辛普森公式

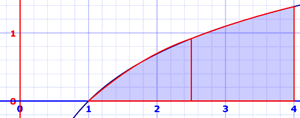
辛普森公式是改良了的梯形法。这个方法是基于梯形法，不过在顶部是抛物线而不是直线。抛物线通常很接近实际的曲线：

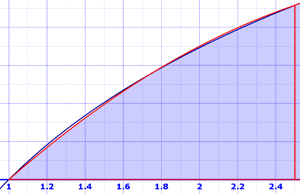
积分近似值：辛普森公式放大

乍看好像很复杂，但最终的公式和梯形法差不多（不同的是除以 3 以及用 4,2,4,2,4 的因子规律）：

Δx 3 × ( f(x₀) + 4f(x₁) + 2f(x₂) + ... 4f(x_n-1) + f(x_n) )

可是：n 一定要是偶数。所以我们试试用 6片，每片的宽都为 0.5：

0.5 3 × ( f(1) + 4f(1.5) + 2f(2) + 4f(2.5) + 2f(3) + 4f(3.5) + f(4) )

代入 ln(1) 等的值，结果是：

0.5 3 × ( 15.2679…… )

2.544648……

与2.545177...相比，这是个很好的答案！

正与负

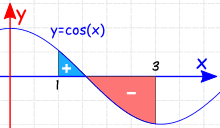
定积分 cos(x) 从1到3

注意当曲线在X轴的下面时，面积是负数。

误差和精确度

我们来比较以上的方法：

f(x)=ln(x)	N = 3		N = 6		N = 100
	近似值	误差	近似值	误差	近似值	误差
左矩形法	1.791759	0.753418	2.183140	0.362037	2.524327	0.020850
右矩形法	3.178054	-0.632877	2.876287	-0.331110	2.565916	-0.020739
中点矩形法	2.574519	-0.029342	2.552851	-0.007674	2.545206	-0.000029
梯形法	2.484907	0.060271	2.529713	0.015464	2.545121	0.000055
辛普森公式	（N 一定要是偶数）		2.544648	0.000529	2.545177	<0.000001

辛普森公式最棒！用起来也不比其他方法复杂。

当然，不同的函数会有不同的结果。你可以自己试试！

最大误差

在实际情况下我们不会知道绝对精确的答案……那么我们怎样知道我们的近似值有多准确呢？

你可以尝试不同宽度的片来大约了解近似值的精确度。

你也可以用以下的公式来求近似值的最大可能误差（结果是最大误差，实际误差可能会比较小）：

中点矩形法：|E| = K(b-a)³ 24n²

梯形法：|E| = K(b-a)³ 12n²

辛普森公式：|E| = M(b-a)⁵ 180n⁴

其中：

|E| 是最大误差的绝对值（误差可以是正数或负数）
a 是区间的起点
b 是区间的终点
n 是片的个数
K 是区间里的最大二阶导数。
M 是区间里的最大四阶导数。

（"最大" 的意思是最大的绝对值。）

求 a、b 和 n 很容易，但怎样求 K 和 M？

例子：f(x) = ln(x) 从 1 到 4

先求一些下面会用到的导数:

一阶导数：f'(x) = 1/x
二阶导数：f''(x) = −1/x²
三阶导数：f⁽³⁾(x) = 2/x³
四阶导数：f⁽⁴⁾(x) = −6/x⁴
五阶导数：f⁽⁵⁾(x) = 24/x⁵

最大的 K 值可能是在起点、终点或中间某个点：

起点：f''(1) = −1/1² = −1
终点：f''(4) = −1/4² = −1/16
中间：用三阶导数来看看从 1 到 4 的区间里有没有零值。如果有的话，就代表有方向改变。
在 1 和 4 之间的某些地方，f⁽³⁾(x) = 0 吗？没有。所以最大值是在起点或终点。

所以 K = 1 （最大的绝对值）

M 也是一样，但用更高的导数：

起点：f⁽⁴⁾(1) = −6/1⁴ = −6
终点：f⁽⁴⁾(4) = −6/4⁴= −6/256
中间：用五阶导数来看看从 1 到 4 的区间里有没有零值。
在 1 和 4 之间的某些地方，f⁽⁵⁾(x) = 24/x⁵ 等于零吗？没有。

所以，M = 6 （最大的绝对值）

在只有 6 片的情况下，最大误差是：

中点矩形法：|E| = 1(4-1)³ 24×6² = 0.03125

梯形法：|E| = 1(4-1)³ 12×6² = 0.0625

辛普森公式：|E| = 6(4-1)⁵ 180×6⁴ = 0.00625

熟悉的图形

曲线可能有我们熟悉的图形，如果是这样，我们便可以用几何公式：

例子：三角形

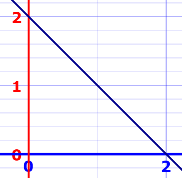
积分近似值三角形
f(x) = 2 − x，从 0 到 2

A = ½ × 2 × 2 = 2

例子：矩形

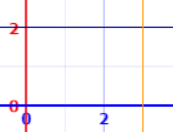
积分近似值矩形
f(x) = 2，从 0 到 3

A = 2 × 3 = 6

例子：半圆形

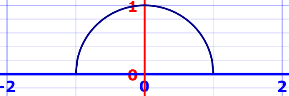
积分近似值半圆形
f(x) = √(1 − x²), 从 −1 到 +1

A = π r² / 2 = π / 2

结论

要估计函数的曲线下面的面积，我们可以把函数切成片

有很多不同的方法去求每一片的面积，例如：

左矩形法
右矩形法
中点矩形法
梯形法
辛普森公式

我们可以用误差公式来求近似值的最大可能误差

基本几何公式有时可以帮助我们求曲线下面的面积