平均差
各个数据值离平均值平均有多远
怎样计算
先求数据的平均值……接着求距离……最后求距离的平均!
三部曲:
- 一、求所有数据值的平均值
- 二、求每个数据与平均值的距离(用数据值减去平均值,不理正负号)
- 三、求这些距离的平均
像这样:
例子:3、6、6、7、8、11、15、16 的 平均差
一、求平均:
| 平均 = | 3 + 6 + 6 + 7 + 8 + 11 + 15 + 16 | = | 72 | = 9 |
| 8 | 8 |
二、求每个数据只与平均值的距离:
| 值 | 与 9 的距离 |
|---|---|
| 3 | 6 |
| 6 | 3 |
| 6 | 3 |
| 7 | 2 |
| 8 | 1 |
| 11 | 2 |
| 15 | 6 |
| 16 | 7 |
像这样:
(没有正负号!)
三、求这些距离的平均:
| 平均差 = | 6 + 3 + 3 + 2 + 1 + 2 + 6 + 7 | = | 30 | = 3.75 |
| 8 | 8 |
所以,平均值 = 9,平均差 = 3.75
平均差告诉我们,每个数据值平均离中心有多远。
在上面的例子里,数据值平均离中心 3.75 远。
在这里,差就是距离
公式
公式是:
平均差 = Σ|x − μ|N
- Σ 是 总和符号,意思是加起来
- || (垂直线)的意思是 绝对值,就是不要正负号
- x 是每个数据值(例如 3 或 16)
- μ 是平均(在这例子里,μ = 9)
- N 是数据点的个数(在这例子里,N = 8)
我们详细看看:
绝对偏差
在公式里求的每个距离是叫绝对偏差,因为它是偏差的绝对值(离平均值的距离)。
我们把 "|" 放在项的两变来代表 "绝对值": |-3| = 3 为每一个 x: 绝对偏差 = |x - μ| |
在这个例子里,16 的 绝对偏差 = |x - μ| = |16 - 9| = |7| = 7
现在把它们加起来……
总和符号
"加起来" 的符号是 Σ(叫总和符号),所以:
绝对偏差的总和 = Σ|x - μ|
除以数据的个数 N,得到:
平均差 = Σ|x − μ| N
我们再用正确的符号做一次:
例子: 3、6、6、7、8、11、15、16 的 平均差
一、求平均:
| μ = | 3 + 6 + 6 + 7 + 8 + 11 + 15 + 16 | = | 72 | = 9 |
| 8 | 8 |
二、求绝对偏差:
| x | |x - μ| |
|---|---|
| 3 | 6 |
| 6 | 3 |
| 6 | 3 |
| 7 | 2 |
| 8 | 1 |
| 11 | 2 |
| 15 | 6 |
| 16 | 7 |
| Σ|x - μ| = 30 |
三、求平均差:
| 平均差 = | Σ|x - μ| | = | 30 | = 3.75 |
| N | 8 |
注意:平均差有时也叫平均绝对偏差(英语 Mean Absolute Deviation (MAD)),因为它是绝对偏差的平均。
平均差的意思是什么?
平均差告诉我们,每个数据值平均离中心有多远。
以下是个例子(用 标准差 网页里的数据):
例子:你和你的朋友测量了你们的狗的身高(毫米):
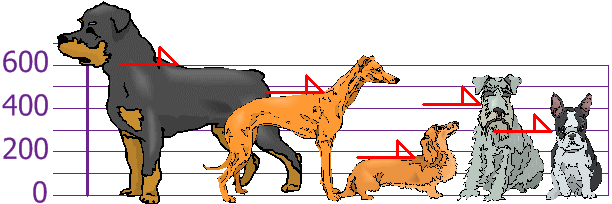
身高(到肩膀)是:600mm、470mm、170mm、430mm 和 300mm。
一、求平均:
| μ = | 600 + 470 + 170 + 430 + 300 | = | 1970 | = 394 |
| 5 | 5 |
二、求绝对偏差:
| x | |x - μ| |
|---|---|
| 600 | 206 |
| 470 | 76 |
| 170 | 224 |
| 430 | 36 |
| 300 | 94 |
| Σ|x - μ| = 636 |
三、求平均差:
| 平均差 = | Σ|x - μ| | = | 636 | = 127.2 |
| N | 5 |
所以,狗的身高与平均值的平均距离是 127.2 mm。
(可以和 147 mm 的标准差比较一下)
检测
在平均值一边的偏差应该和另一边的偏差是相等的。
上面的例子:
例子:3、6、6、7、8、11、15、16
偏差是:
| 6 + 3 + 3 + 2 + 1 | = | 2 + 6 + 7 |
| 15 | = | 15 |
同样:
例子:狗
平均左边的偏差:224 + 94 = 318
平均右边的偏差:206 + 76 + 36 = 318
如果它们不相同……你便是做错了!