条件概率
怎样处理相关事件
我们在生活中时常都会遇到随机事件。你需要对这些事件有个"感觉",才能成为一个聪明和成功的人。
独立事弹子 玻璃球件
事件可以是 "独立" 的,意思是每个事件是 不 受其他事件影响的。

例子:抛硬币。
每一次抛硬币都是绝对独立的。
过去的抛掷对这次抛掷是完全没有影响的。
每一个抛掷得到正面(或反面)的可能性永远是二分之一,或 50%。
每一个抛掷都是个独立事件。
相关事件
但事件也可以是 "相关" 的……意思是 受过去事件影响的……
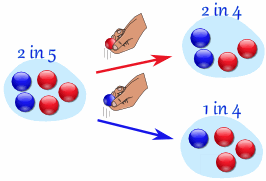
例子:布袋里的弹子
布袋里有 2颗蓝色弹子和 3颗红色弹子。
随机拿一颗,拿到蓝色的概率是多少?
可能性是 五分之二
但拿掉一颗之后情形便不同了!
所以拿第二个的时候:
- 如果第一次拿的是红的,第二次拿到蓝弹子的可能性是四分之二
- 如果第一次拿到是蓝的,第二次拿到蓝弹子的可能性是四分之一
可能性每次都可能改变。每个事件和上一个事件是有关联的,这些事件便是相关的。
我们在这里就是讲这个。
树图
树图:是个显示类似情况的好方法。我们现在为这个弹子例子做个树图。
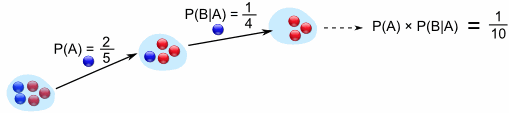
有 2/5 的可能性会拿到蓝弹子,3/5 的可能性会拿到红弹子:
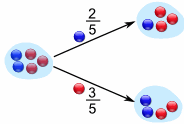
我们来看看拿第二颗弹子时的情形:
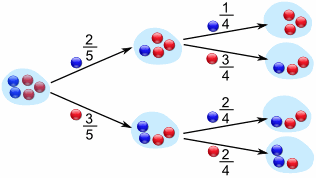
若先拿的是蓝色,第二颗是蓝色的可能性是 1/4,第二颗是红色的可能性是 3/4。
若先拿的是红色,第二颗是蓝色的可能性是 2/4,第二颗是红色的可能性是 2/4。
现在我们可以尝试解答像这样的问题了:"拿到 2颗蓝弹子的可能性是多少?"
答案:2/5 的可能性和之后 1/4 的可能性一起:
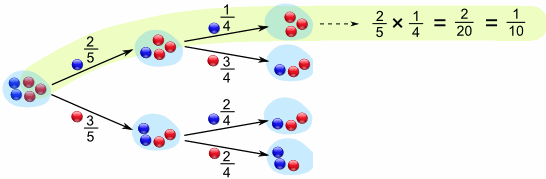
注意我们把可能性相乘,结果是 1/10。
拿到 2颗蓝弹子的可能性是 1/10
记法
数学用很多记法!我们可以用代数来处理这些概念,概率的记法是:
P(A) 的意思是 "事件 A 的概率"
在以上的例子,事件 A 是 "第一次拿蓝色",概率是 2/5:
P(A) = 2/5
事件 B 是 "第二次拿蓝色" …… 有 2个可能:
- 如果第一次拿到的是蓝色,第二次拿蓝色的可能性是 1/4
- 如果第一次拿到的是红色,第二次拿蓝色的可能性是 2/4
所以我们要说明我们想要哪个可能,并用这个符号:"|" 来表示 "在以下发生的条件下":
P(B|A) 的意思是 "在事件 A 发生的条件下,事件 B 发生的概率"
换句话说,事件 A 已经发生了,现在事件 B 发生的可能性是多少?
P(B|A) 也叫在 A 发生的情况下 B 发生的 "条件概率"。
在这个例子里:
P(B|A) = 1/4
所以拿到 2个蓝弹子的概率是:
我们这样写
"事件 A 与 事件 B 的概率等于
事件 A 的概率乘以在事件 A 发生的条件下,事件 B 发生的概率"
我们再写一遍,这次全部用记法:
例子:在一副扑克牌里拿 2张国王
事件 A 是第一次拿一张国王,事件 B 是第二次拿一张国王。
第一张牌是国王的可能性是52分之4(52张牌里有4张国王):
P(A) = 4/52
拿走第一张国王后,第二张是国王的可能性降低了(剩下的51张牌里只有3张是国王):
P(B|A) = 3/51
所以:
P(A 与 B) = P(A) × P(B|A) = (4/52) × (3/51) = 12/2652 = 1/221
所以拿到2张国王的可能性是221分之1,或大约 0.5%
寻找隐藏数据
我们可以用代数来改变一个公式的"主語",像这样:
| 开始: | P(A 与 B) = P(A) × P(B|A) | |
| 换边: | P(A) × P(B|A) = P(A 与 B) | |
| 除以 P(A): | P(B|A) = P(A 与 B) / P(A) |
得到另一个有用的公式:
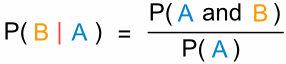
"在事件 A 发生的条件下事件 B 发生的概率等于
事件 A 与事件 B 的概率除以事件 A的概率
例子:冰淇淋
在你的社交群组里,70% 喜欢巧克力冰淇淋,35% 喜欢巧克力和草莓。
在喜欢巧克力的人里,也喜欢草莓的百分比是多少?
P(草莓|巧克力) = P(巧克力 与 草莓) / P(巧克力)
在喜欢巧克力的人里,50% 也喜欢草莓

复杂例子:足球赛
你去踢足球,你想当守门员,但这和今天谁是教练有关:
- 如果是小山做教练,你当守门员的可能性是 0.5
- 如果是阿力做教练,你当守门员的可能性是 0.3
小山更经常做教练……大约每10场球赛有6场是他做教练(概率是 0.6)。
你今天当守门员的概率是多少?
我们来做个树图。首先,写下两个教练的名字:小山 或 阿力:
小山做教练的概率是 0.6,所以阿力做教练的概率是 0.4 (加起来是 1)
如果小山做教练,你有 0.5 的可能性当守门员(0.5 的可能性不当守门员):
如果阿力做教练,你有 0.3 的可能性当守门员(0.7 的可能性不当守门员):
树图做好了,我们可以求概率了。公式是:
P(A 与 B) = P(A) x P(B|A)
这是 "小山,是" 的分支的计算:
(小山做教练的 0.6 的概率乘以小山让你当守门员的 0.5 的概率等于 0.3 的概率。)
还没做完!还要算阿力做教练的情况:
阿力有 0.4 的可能性做教练,让你当守门员的可能性是 0.3,相乘是 0.12
两个 "是" 的分支合到一起:
你有 0.3 + 0.12 = 0.42 的概率今天当守门员
(42% 的可能性)
检验
最后:完成计算后,看看加起来是不是等于 1:
0.3 + 0.3 + 0.12 + 0.28 = 1
对了,加起来是 1,所以计算应该没错。
朋友和随机数
这是一个另类的条件概率的例子。
4个朋友(小李、蛮牛、小王 和 大山),每人从1到5之间随机选一个数。他们其中任何两个人选中相同数字的可能性是多少?
我们逐个来……
首先,小李和蛮牛选同一个数的可能性是多少?
蛮牛把他的数和小李的数比较。相同的可能性是5分之1。
树图是这样的:
注意:"是" 和 "否" 加起来是 1
(1/5 + 4/5 = 5/5 = 1)
现在把小王也算进去……
有两个可能:
- 如果小李和蛮牛的数是相同的,小王只有一个数来和他的数比较。
- 但如果小李和蛮牛的数不是相同的,小王便有两个数来比较。
结果是:
在最上面的一行(小李和蛮牛的数是相同的)已经有两个数相同(可能性是 1/5)。
但如果"小李和蛮牛的数不是相同的",小王的数便有 2/5 的可能性和其中一个数相同(因为小王可以选小李或蛮牛的数)。
我们可以把概率相乘来求合并(两个事件一同发生)的概率:
沿着 "否,是" 的分支……"否"的可能性是 4/5,接着的"是"的可能性是 2/5:
沿着 "否,否" 的分支……"否"的可能性是 4/5,接着的"否"的可能性是 3/5:
注意所有的概率加起来还是 1(这是检查我们有没有算错的好方法):
(5/25) + (8/25) + (12/25) = 25/25 = 1
如果我们把大山也算进去呢?
一样的概念,不过要做更多计算:
做好了,"是" 的概率加起来是 101/125:
答案:101/125
但有个有趣的捷径……我们可以沿着"否"的分支做,便可以省掉其他的计算,做起来也简单很多:
没有相同的数的可能性是:
(4/5) × (3/5) × (2/5) = 24/125
所以有相同的数的可能性是:
1 - (24/125) = 101/125
(连树图也不需要!)
这是在解概率问题常用的技巧:
通常计算"否"的概率是比较容易的
(用 1 减去"否"的概率就是"是"的概率)
(我们在 同一个生日 这网页里有这个技巧的具体说明。)