活动：时钟和角度

这活动是关于 针式时 钟 以及钟上时针和分针形成的角度。你可在度数（角）找到更多关于角度和测量角度的信息。

 

一点钟时，时钟上的时针和分针形成的角度是什么？

一点钟时，分针（红色）指着 12，时针（蓝）指着 1. 所以我们要算 12 和 1 之间的角度。

这个角度，在一整个圈里有几个？

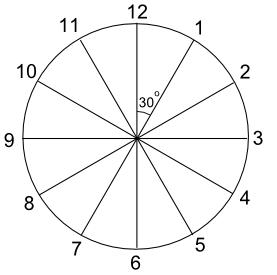
一整圈（360°） 里有 12 个这样的角度，所以一个角度是 360° ÷ 12 = 30°

一点钟时，时钟上的长短针形成的角度是 30°。

两点半时，时钟上的时针和分短针形成的角度是什么？

在这个时候，分针和时针中间有几个 30° ？

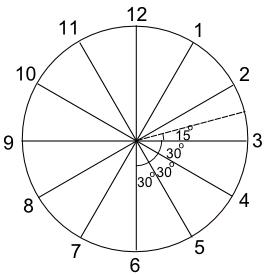
• 5 和 6 之间的角度是 30°
• 4 和 5 之间的角度是 30°
• 3 和 4 之间的角度是 30°
• 剩下的角度是 ½ × 30° = 15°

所以在两点半，时针和分针之间的角度 = 30° + 30° + 30° + 15° = 105°

 

轮到你了

完成以下列表 (用较小的角度）：

时间	1:00	2:30	7:00	10:30	11:20	3:40	5:15	8:45
角度	30°	105°

你可在这页的页底找到答案。

 

比较复杂的时间

只要时间不复杂，计算长短针之间的角度就很容易。

但是，计算在 9:37 时长短针之间的角度就难多了。你可以试试，但这可能太困难了。

例子： 什么时候长短针之间的角度是 30°?

留意这问题问的是 “时间'。答案有好几个，有些容易找到，有些困难很多。

这是两个容易的答案：

 

一点钟	十一点钟
这个呢？
4:15

 

乍看，这好像也是 30°，但在 4:15 时，时针已经在 4 和 5 之间走了四分之一。

所以角度是 30° + ¼ × 30° = 30° + 7½° = 37½°.

这是比较准确的答案：

你可不可以找到像这样的 30° 角？

 

什么时候长短针形成一直线？

即，它们之间的角度是 180°？

一个显而易见的答案是 6 点钟：

 

但有没有其他答案？

9:15 不对，原因和 4:15 不是 30° 一样。。。。。。时针已走过了 9 字。

这好像是个非常困难的问题，但其实有简单的方法去解答。

从上午 6:00 到下午 6:00， 时针和分针有多少次形成直线？

每小时最少有一次：:

• 上午 7:00 到 8:00 一次，
• 上午 8:00 到 9:00 一次，
• 上午 9:00 到 10:00 一次，
• 等等，直至。。。。。。
• 下午 4:00 到 5:00 一次，

这是 11 个同样长短的时段，所以：

上午 6:00 后，时针和分针第一次形成直线大约是在上午 7:05½ ：

轮到你了!

时	上午 7 − 8	上午 8 − 9	上午 9 − 10	上午 10 − 11	上午 11 − 12	下午 12 − 1	下午 1 − 2	下午 2 − 3	下午 3 − 4	下午 4 − 5
时间	上午 7:05½

你可以去模拟和数字时钟动画 检查你的答案

 

你可以计算什么时候时针和分针成直角吗？

（提示：有 22 个这样的时间）

 

上面练习题的答案:

时间	1:00	2:30	7:00	10:30	11:20	3:40	5:15	8:45
角度	30°	105°	150°	135°	140°	130°	67½°	7½°