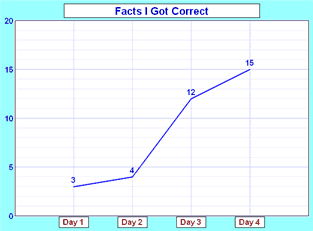
活动:柯尼斯堡七桥问题
柯尼斯堡古镇有七座桥:
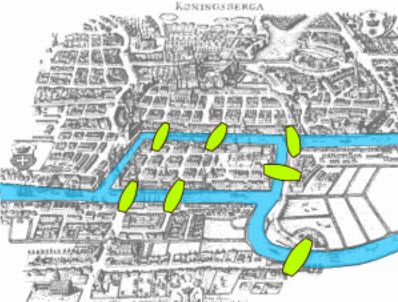
你可不可以步行经过
城镇每一部分,
但只 通过每座桥一次?
一个叫莱昂哈德·欧拉的著名数学家研究过这问题。。。。。。但我们自己来寻找答案!
在这过程中我们也会学到一些 "图论"。
简化它
我们可以简化以上的地图成为:
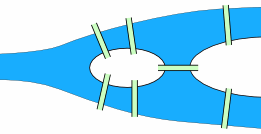
城镇有四部分-―― 河北边的大陆、河南边的大陆、 小岛和半岛 (右边的陆地)
将它们标记为 A, B, C 和 D:
要 “经过” 城镇的 每一部分",你要经过 A, B, C 和 D。 同时你要通过每座桥 p, q, r, s, t, u 和 v 各一次。 |
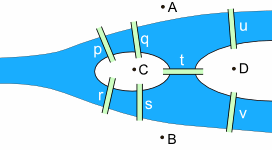 |
我们可以再简化成这样:
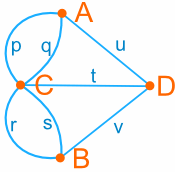
你不用在镇里走路了,
你只需用笔画线。
轮到你了
你可不可以每条线, p, q, r, s, t, u 和 v 只画一次,一笔画,笔不离纸 (你可在任何地方开始) ?
试试看。
。。。。。。
成功了吗?
好。。。。。。我们先从简单的图开始。
试试这些 (记得: 画所有的线,但不要重复任何线,同时笔不离纸。)
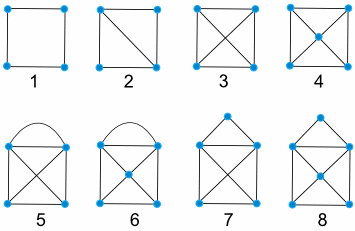
记下结果:
| 形状 | 成功? |
| 1 | 是 |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 |
我们怎样知道哪个是对的,哪个是错的?
研究一下!
先学一些特别名词:
|
 |
对,这叫 “图”。。。。。。但不是 这样的图: 两种都叫
“图”。 |
 |
 |
|
|
 |
例子:
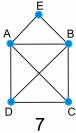 |
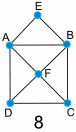 |
图 7 有
|
图 7 有
|
欧拉路径
想像线条是桥。如果你通过每条一次问题就解决了,所以。。。。。。
。。。。。。我们要找一条“欧拉路径”。。。。。。
提示: 度数是单数的顶点的数目可以告诉我们哪个图有“欧拉路径”.
填这列表:
| 形状 | 欧拉路径? | 顶点 | 双数度数有几个 | 单数度数有几个 |
| 1 | 是 | 4 | 4 | 0 |
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 |
有规率吗?
在你找到规率前,不要看下去。。。。。。答案在列表里。
好了。。。。。。答案是。。。。。。
度数是单数的顶点的数目一定要是零或二。
如果不是这样,便没有“欧拉路径”
同时,如果有两个顶点的度数是单数,它们就是起点和终点。
理由其实不难理解。
路径经过一条边缘进去顶点,也经过另外一条边缘离开。
所以边缘都是一双双的(双数)。
只有起点和终点可以有单数度数。
我们再看看七桥问题 :

顶点 A、 B 和 D 的度数是
3,顶点 C 的度数是
5, 所以这图有四个顶点是单数度数的。 所以它 没有欧拉路径。
我们解答了七桥问题了,就像三百年前的欧拉一样!
额外练习: 下面的图哪个有欧拉路径?
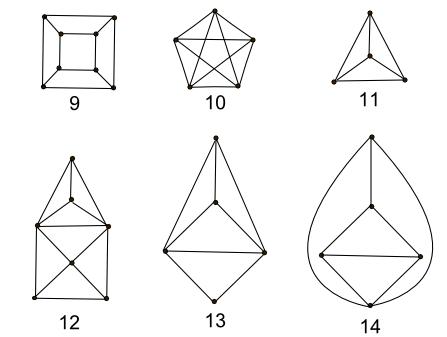
| 形状 | 欧拉路径 | 顶点 | 双数度数有几个 | 单数度数有几个 |
| 9 | ||||
| 10 | ||||
| 11 | ||||
| 12 | ||||
| 13 | ||||
| 14 |
脚注
莱昂哈德·欧拉 (1707 - 1783),瑞士数学家, 是有史以来最伟大和著作最多的数学家之一。 欧拉一生大部分时间在柏林科学院工作,他就在那里解答了“柯尼斯堡七桥问题”。
柯尼斯堡城镇 横跨普里高里河。它以前是在普鲁士,但现在叫加里宁格勒,是俄国的一部分。 柯尼斯堡的位置邻近河口,有七座桥连着河的两边,还有一个小岛和半岛。
图列表 的答案:
| 形状 | 成功? | 双数 | 单数 |
| 1 | 是 | 4 | 0 |
| 2 | 是 | 2 | 2 |
| 3 | 否 | 0 | 4 |
| 4 | 否 | 1 | 4 |
| 5 | 是 | 2 | 2 |
| 6 | 是 | 3 | 2 |
| 7 | 是 | 3 | 2 |
| 8 | 是 | 4 | 2 |