方程的对称
方程可以是对称的:
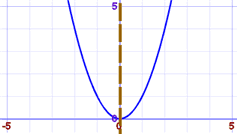 |
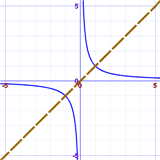 |
| x2的图 | 1/x 的图 |
| 沿y轴对称 | 对角对称 |
换句话说,有镜像关系。
好处
在方程里找对称的好处是:
- 我们可以更了解方程
- 画图更容易
- 可以帮助我们去解方程。当我们在一边找到解时,我们便可以说"基于对称关系,(镜像值)……"
怎样检测对称
通常留心过观察就会知道,但如要确实,我们便需要做一个简单的检测:
用对称的值时方程是否没有改变?
具体做这个检测的方法与对称的各类有关:
沿y轴对称
如果对称是沿y轴对称,需要检测用 −x 代替 x 后,方程是否保持不变:
沿x轴对称
和是沿y轴对称一样,但尝试以 −y 来代替 y。
例子:y = x3 是不是是沿x轴对称?
尝试以 −y 来代替 y :
−y = x3
现在试试可不可以得到原来的方程:
每边乘以 −1:
y = −x3
这和原来的方程不同
故此,y = x3 不是 是沿x轴对称
对角对称
试试把 y 和 x 互换(就是,以 x 代替 y 和 以 y 代替 x)。
例子:y = 1/x 是对角对称的吗?
开始:
y = 1/x
y 和 x 对换:
x = 1/y
重排:每边乘以 y:
xy = 1
每边除以 x:
y = 1/x
得到原来的方程。
故此,y = 1/x 是对角对称的
原点对称
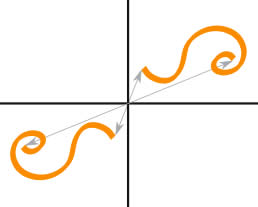 |
原点对称 的意思是每个部分都有相对的部分,而这相对部分是:
|
检测:试着 −x 代替 x 和以 −y 代替 y 后,方程有没有改变。
例子:y = 1/x 是原点对称的吗?
开始:
y = 1/x
以 −x 代替 x,并以 −y 代替 y:
(−y) = 1/(−x)
每边乘以 −1:
y = 1/x
得到原来的方程。
故此,y = 1/x 有 原点对称
惊艳! y = 1/x 既是原点对称又是对角对称的!