指数增长和衰减
神奇的指数增长!

想象有一棵神奇的树。
高度(mm) = ex
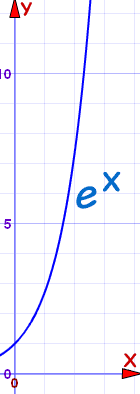
- 一岁大时,它有:e1 = 2.7 mm 高……非常矮小!
- 五岁时,它有:e5 = 148 mm 高……大概一个杯子那么高
- 十岁:e10 = 22 m 高……房子那么高
- 十五岁:e15 = 3.3 km 高……比巴黎铁塔高十倍
- 二十岁:e20 = 485 km 高……到外太空了!
没有树能长这么高!
所以当人家说:"以指数级增长"……你需要想想那究竟是什么意思。
但有时物体真的可以以指数级增长(或相反:衰减),至少在一段时间里可以。
有一个有用的通用公式:
y(t) = a × ekt
其中: y(t) = 时间等于 "t"时的值
a = 开始的值
k = 增长率(>0)或 衰减(<0)
t = 时间
例子:2个月前你有3只小老鼠,现在你有18只。
 |
假设数目一直按这个速度增长
|
从这公式开始:
y(t) = a × ekt
我们知道a=3只小老鼠,t=2个月,并且现在 y(2)=18只小老鼠:
18 = 3 × e2k
用代数来解 k:
| 每边除以 3: | 6 = e2k | |
| 取每边的自然对数: | ln(6) = ln(e2k) | |
| ln(ex)=x,故此: | ln(6) = 2k | |
| 重排: | k = ln(6)/2 |
(注意:k ≈ 0.896,但最好是把它一直保留在 ln(6)/2 的格式,直到最后的计算。)
我们想知道再过两个月(当 t=4个月)及一年后(t=14个月),小老鼠的数量是多少:
y(4) = 3 e(ln(6)/2)×4 = 108
y(14) = 3 e(ln(6)/2)×14 = 839,808
哈!很多小老鼠!你打算怎样喂它们?
指数衰减
有些东西以指数级"衰减"(减少)。
例子:大气压(你周围的空气的压力)随着海拔高度而减小。
每 1000米它以指数衰减大约 12%。
在海平面,大气压是大约 1013 hPa (与天气有关)。

- 写下公式,包括("k"值在内),
- 求在美国帝国大厦屋顶(381米)的大气压,
- 和在珠穆朗玛峰顶 (8848米)的大气压
从这个公式开始:
y(t) = a × ekt
我们知道
- a(海平面的大气压) = 1013 hPa
- t 的单位是米(距离,不是时间,但公式仍然适用)
- y(1000) 是 1013 hPa 减少了 12%= 891.44 hPa
所以:
891.44 = 1013 ek×1000
用代数来解 k:
| 每边除以 1013: | 0.88 = e1000k | |
| 我们知道 | ln(0.88) = ln(e1000k) | |
| ln(ex)=x,故此: | ln(0.88) = 1000k | |
| 重排: | k = ln(0.88)/1000 |
解了 "k",我们可以写成:
y(t) = 1013 e(ln(0.88)/1000)×t
现在我们可以计算在 381米 和 8848米的大气压:
y(381) = 1013 e(ln(0.88)/1000)×381 = 965 hPa
y(8848) = 1013 e(ln(0.88)/1000)×8848 = 327 hPa
(在珠穆朗玛峰顶的实际大气压是大约 337 hPa……我们的计算不赖!)