圆定理
角与圆的一些有趣事实。
圆周角
首先,一个定义;
圆周角:由圆周上的点所形成的角。
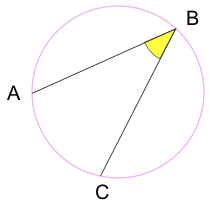
A 和 C 是 "端点"
B 是 "顶点"
关于圆周角的定理
圆周角 a°是圆心角 2a°的一半
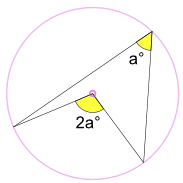
(这叫圆心角定理)
并且(固定端点)……
……角 a° 是不变的,不管顶点在圆周的哪个位置:
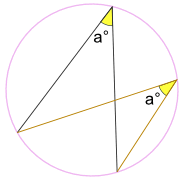
角 a° 永远不变。
(这叫同弓形內的圆周角定理)
例子:角POQ 是多大?(O 是圆心)
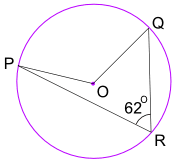
角POQ = 2 × 角PRQ = 2 × 62° = 124°
例子:角CBX 是多大?
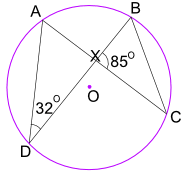
角ADB = 32°,等于角ACB。
角ACB 也等于角XCB。
所以在 BXC 三角形中,角BXC = 85°,角XCB = 32°
三角形的内角的和是 180°:
角CBX + 角BXC + 角XCB = 180°
角CBX + 85° + 32° = 180°
角CBX = 63°
半圆上的圆周角
半圆上的圆周角永远是个直角:
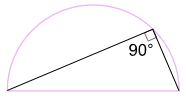
(端点在直径的两端,
顶点在圆周的任何一点。)
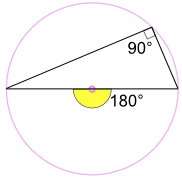
为什么?因为: 圆周角90°是圆心角 180° 的一半 (用"圆心角定理") |
 |
另一个推论
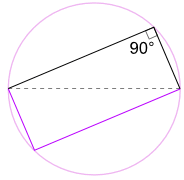
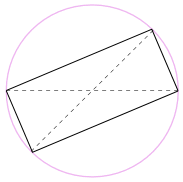
我们也可以把图形旋转 180°来形成一个矩形!
这是个矩形,因为对边是平行的,并且对角线是等长的。
所以所有内角都是直角(90°)。
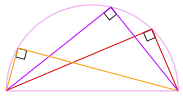
所以不管在圆周上哪一点,
角都是 90°
例子:角BAC 是多大?
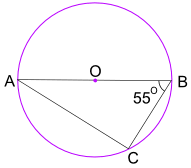
根据半圆上的圆周角定理,角ACB = 90°
三角形的内角的和是 180°,所以:
角BAC + 55° + 90° = 180°
角BAC = 35°
圆内接四边形
"圆内接"四边形的四个顶点都在圆周上: |
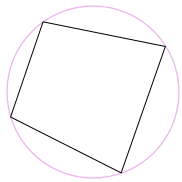 |
圆内接四边形的对角的和是 180°:
|
例子:角WXY 是多大?
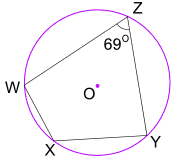
圆内接四边形的对角的和是 180°
角WZY + 角WXY = 180°
69° + 角WXY = 180°
角WXY = 111°
切线角切线是刚好在一点接触圆的直线。 切线与圆的半径永远是垂直的(成直角)。 |