测量的误差
 |
误差? 不……你不是测量错了……这是关于准度。 |
测量仪器不是绝对准确的!
准度
准度与测量仪器是有关联的。一般来说:
例子:
| 如果测量仪器的单位是 "1", 任何在 6½ 与 7½ 之间的值都会被测量为 "7" |
 |
| 如果测量仪器的单位是 "2", 任何在 7 与 9 之间的值都会被测量为 "8" |
 |
注意箭头指着同一个位置,但测量结果是不同的!
加或减
| 我们可以用 "加减" 符号来表表示误差: | ± |
当数值是在 6½ 与 7½之间时 7 ±0.5 误差是 ±0.5 |
 |
当数值是在 7 与 9 之间时 8 ±1 误差是 ±1 |
 |

例子:栅栏的测量长度是 12.5米,准确到 0.1米
准确到 0.1米的意思是真实的值可能是在每边的 0.05米 之内:
长度 = 12.5 ±0.05米
所以长度可能是在 12.45米和 12.55米之间的任何值。
绝对、相对和百分比误差
我们不知道真实值,所以我们只能用测量值:
| 相对误差 = | 绝对误差 |
| 测量值 |
我们用个例子看看:

例子:栅栏(续)
长度 = 12.5 ±0.05米
所以:
绝对误差 = 0.05米
所以:
| 相对误差 = | 0.05米 | = 0.004 |
| 12.5米 |
也就是:
百分比误差 = 0.4%
更多例子:

例子:温度计测量到最近的 2度。测量结果是 38°C
温度可能是 38°每边浮动 1°(就是在 37°与 39°之间)
温度 = 38 ±1°
所以:
绝对误差 = 1°
并且:
| 相对误差 = | 1° | = 0.0263…… |
| 38° |
也就是:
百分比误差 = 2.63……%
例子:你测量到植物是 80厘米高(到最近的厘米)
这代表你的误差最大可以是 0.5厘米(植物的高度是在 79.5 与 80.5厘米之间)
高度 = 80 ±0.5厘米
所以:
绝对误差 = 0.5厘米
并且:
| 相对误差 = | 0.5厘米 | = 0.00625 |
| 80厘米 |
也就是:
百分比误差 = 0.625%
面积
处理面积时你需要考虑长度和宽度……它们可以都是最小值,也可以都是最大值。
例子:小李测量田地的大小:长度是 6米,宽度是 8米(到最近的米)。
测量到最近的米代表结果可能大了或小了半米。
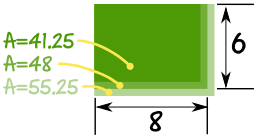
宽度(w)可以是从 5.5米到 6.5米:
长度(l)可以是从 7.5米到 8.5米:
面积是宽度 × 长度:
面积最小可以是:5.5米 × 7.5米 = 41.25 平方米
测量的面积是:6米 × 8米 = 48平方米
面积最大可以是:6.5米m × 8.5米 = 55.25平方米
面积的绝对、相对和百分比误差
巧妙的是……绝对误差是多少?
- 从 41.25 到 48 = 6.75
- 从 48 到 55.25 = 7.25
答案:选大的!所以:
绝对误差 = 7.25平方米
| 相对误差 = | 7.25平方米 | = 0.151…… |
| 48平方米 |
百分比误差 = 15.1%
(不大准确!)
体积
体积需要三个测量:宽度、长度、高度!
例子:大山测量箱子的尺寸到最近的 2厘米,测量值是 24厘米 × 24厘米 × 20厘米
测量到最近的 2厘米就是说真实值可以大于或小与测量值 1厘米。
三个测量结果是:
- 24 ±1厘米
- 24 ±1厘米
- 20 ±1厘米
体积是 宽度 × 长度 × 高度:
体积最小可以是:23厘米 × 23厘米 × 19厘米 = 10051 立方厘米
测量到的体积是:24厘米 × 24厘米 × 20厘米 = 11520立方厘米
体积最大可以是:25厘米 × 25厘米 × 21厘米 = 13125立方厘米

我们得到的结果是:
体积的绝对、相对和百分比误差
绝对误差:
- 从 10051 到 11520 = 1469
- 从 11520 到 13125 = 1605
选大的:
绝对误差 = 1605立方厘米
| 相对误差 = | 1605立方厘米 | = 0.139…… |
| 11520立方厘米 |
百分比误差 = 13.9%