Three Vessels Puzzle - Solution
The Puzzle:
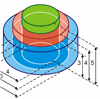
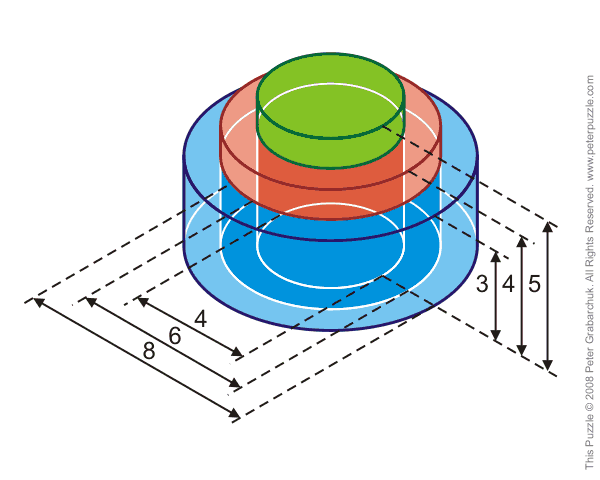
There are three different color cylindrical vessels: Blue, Red, and Green, with the sizes, as shown.
The Red vessel is put into the Blue one, and the Green vessel into the Red one as shown.
Each vessel is full of water.
Which vessel contains the largest quantity of water?
You can ignore the thickness of the walls of the vessels.
Author: Peter Grabarchuk
This Puzzle © 2008 Peter Grabarchuk. All Rights Reserved.
More from Peter Grabarchuk at PeterPuzzle.com
The Red vessel is put into the Blue one, and the Green vessel into the Red one as shown.
Each vessel is full of water.
Which vessel contains the largest quantity of water?
You can ignore the thickness of the walls of the vessels.

Author: Peter Grabarchuk
This Puzzle © 2008 Peter Grabarchuk. All Rights Reserved.
More from Peter Grabarchuk at PeterPuzzle.com
Our Solution:
Radius of green vessel = 4/2 = 2
Radius of red vessel = 6/2 = 3
Radius of blue vessel = 8/2 = 4
Volume of green vessel on its own = π × 22 × 5 = 20π
Volume of red vessel on its own = π × 32 × 4 = 36π
Volume of blue vessel on its own = π × 42 × 3 = 48π
Volume of water in green vessel = 20π
Volume of water in red vessel = Volume of red vessel - 4/5 × Volume of green vessel = 36π - 16π = 20π
Volume of water in blue vessel = Volume of blue vessel - 3/4 × Volume of red vessel = 48π - 27π = 21π
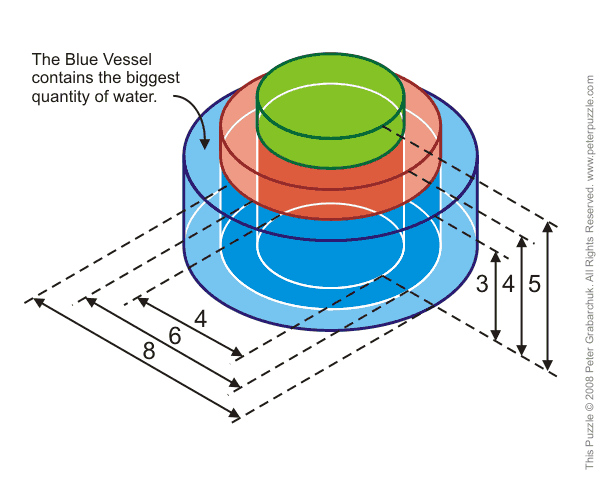
So the Blue Vessel contains the largest quantity of water.
Author: Peter Grabarchuk
This Puzzle © 2008 Peter Grabarchuk. All Rights Reserved.
Radius of red vessel = 6/2 = 3
Radius of blue vessel = 8/2 = 4
Volume of green vessel on its own = π × 22 × 5 = 20π
Volume of red vessel on its own = π × 32 × 4 = 36π
Volume of blue vessel on its own = π × 42 × 3 = 48π
Volume of water in green vessel = 20π
Volume of water in red vessel = Volume of red vessel - 4/5 × Volume of green vessel = 36π - 16π = 20π
Volume of water in blue vessel = Volume of blue vessel - 3/4 × Volume of red vessel = 48π - 27π = 21π
So the Blue Vessel contains the largest quantity of water.

Author: Peter Grabarchuk
This Puzzle © 2008 Peter Grabarchuk. All Rights Reserved.
Puzzle Author: Grabarchuk, Peter
See this puzzle without solution
Discuss this puzzle at the Math is Fun Forum