活动: 用骰子做实验
你需要:
|
 |
有趣的是
很多人以为一个骰子(单数)在英语叫 "a dice"。 不对!
复数 is dice,但单数是 die。 (就是, 1 die, 2 dice。)
常见的骰子有六面:
通常这六面是叫 1, 2, 3, 4, 5 和 6。
高,低,最可能
开始前,想想可能发生什么。
问题: 若你掷一个骰子:
- 1。 最 小 的得分是什么?
- 2。 最 大 的得分是什么?
- 3。 你觉得 最可能 的得分是什么?
前两个问题很容易:
- 1。 最小 的得分是 1
- 2。 最大 的得分是 6
- 3。 最可能 的得分是。。。。。。???
所有的得分都同样可能吗? 还是有些得分会发生多一点?
我们来看看什么是最可能的。。。。。。
实验
掷 一个骰子
60 次,把得分
记录 在计数表上。
你可以用 计数符号来记录得分:
| 得分 | 计数符号 | 次数 |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 总次数 = | 60 |
好,开始!
。。。 。。。
完了 。。。? 画一个柱状图来显示及说明你的结果。 填入这个表格: 你也可以用 数据图
(柱状图、线状图和饼状图) |
 |
|
|
你的结果可能像这样:
|
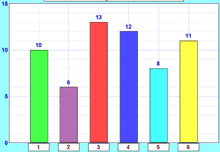 |
- 所有条线都一样高吗?
- 如果不是。。。 。。。为什么?
掷 60 次
好, 我为什么叫你掷 60 次? 6 次是不够的,得不到好结果。 600 次会给你很好的结果,但太费时了。 所以 60 次就差不多了, 同时也是 10 组,每组 6 次。
所以我们 期望 每个数字10 次,像这样:
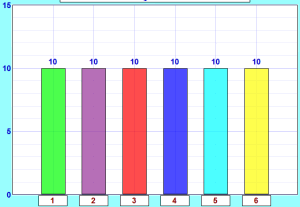
这是 理论 值,
与你在 实验 中得到的 实验值不一样!
理论值和你的实验值比较起来怎么样?
这图和你的图应该 相似,但它们应该不会完全一样,因为你的实验有 偶然性,同时你掷的次数亦相当小。
若你重复很多次这实验,你的实验结果便会相当接近理论值。
问题
- 最多掷得哪一面? ____
- 最少掷得哪一面? ____
- 若你重复这实验,结果会一样吗? 会 / 不会
做实验得到结果。
重复实验可能会得到 不同的 结果!
故此重要的是,要知道何时结果是 高质量的, 或只是 随机的。
概率
在 概率 页上有一个公式:
一起事项发生的概率 = 它可以发生的方法的数目所有结果的数目
例子: 2 的概率
有 6 个可能的结果。
只有 1 个方法可得到 2。
所以,得到 2 的概率是:
2 的概率 = 16
每个得分都做一次:
| 得分 | 概率 |
| 1 | 1/6 |
| 2 | 1/6 |
| 3 | 1/6 |
| 4 | 1/6 |
| 5 | 1/6 |
| 6 | 1/6 |
| 总和 = 1 |
所有概率的和是 1
任何实验:
所有 可能结果的概率的和是 1