活动: 用骰子做实验
掷两个骰子,把两个得分加起来。。。。。。
你需要:
|
 |
有趣的问题
很多人以为一个骰子(单数)在英语叫 “a dice”。 不对!
复数是 dice, 但单数是 die: 就是,1 die, 2 dice。
常见的骰子有六面:
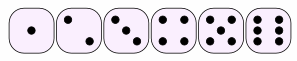
通常这六面是叫 1, 2, 3, 4, 5 和 6。
掷两个骰子,把两个得分加起来。。。。。。
例子: 一个骰子是 2,另外一个是 6, 总得分是 2 + 6 = 8
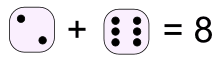
问题: 有其他方法可得到 8 吗?
这个: 6 + 2 = 8 (反过来),这是不同的方法吗?
是! 因为两个骰子是不同的。
例子: 想像一个骰子是红的,另外一个是蓝的。
有两个可能:
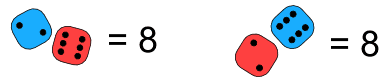
所以 2 + 6 和 6 + 2 是不同的。
你亦可以用其他的数目来得到 8 , 例如 3 + 5 = 8 和 4 + 4 = 8
高,低,最可能
开始前,想想可能发生什么。
问题: 若你一起掷两个骰子,然后加起得分:
- 1。 最 小 的得分是什么?
- 2。 最 大 的得分是什么?
- 3。 你觉得 最可能 的得分是什么?
前两个问题很容易:
- 1。 最小 的得分是 1 + 1 = 2
- 2。 最大 的得分是 6 + 6 = 12
- 3。 最可能 的得分是。。。。。。 ???
所有的得分都同样可能吗? 还是有些得分会发生多一点?
我们做个实验来帮我们解答第三条问题。
实验
一起掷 两个骰子
108 次,每次把两个骰子掷出来的数字
加起来 ,
记下 得分在计数表上。
为什么 108 次? 好像一个奇怪的数字。 待会我来解释。
用 计数符号填这个表格:
| 得分 (两骰的和) |
计数符号 | 次数 |
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 总值 = | 108 |
好, 开始!
。。。。。。
。。。。。。
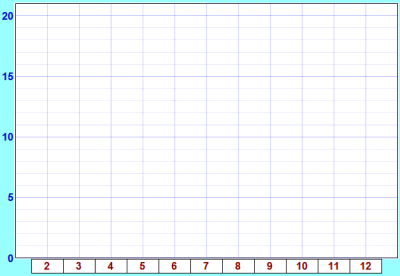
完了。。。? 画一个柱状图来显示说明你的结果。 你也可以用 数据图 (柱状图、线状图和饼状图) ,把图打印。 |
 |
|
你的结果可能像这样:
|
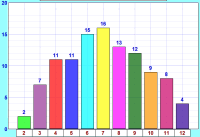 |
- 所有柱子都一样高吗?
- 如果不是。。。 。。。为什么?
为什么是这个形状?
解释很简单:
- 只有 一 个方法得到 2 (1 + 1),
- 但有 六 个方法得到 7 (1 + 6, 2 + 5, 3 + 4, 4 + 3, 5 + 2 和 6 + 1)
以下的列表列出所有可能的结果和总数。 我也用 黑体字显示出怎样可以得到 7。
| 一个骰子的得分 | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | ||
另一个 骰子的 得分 |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
你可看到只有 1 个方法去得到 2, 2 个方法去得到 3,以此类推。
我们数数有几个方法来得到每个得分,填在表里:
| 总 得分 |
多少个 方法可以得到 这分数 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| 6 | 5 |
| 7 | 6 |
| 8 | 5 |
| 9 | 4 |
| 10 | 3 |
| 11 | 2 |
| 12 | 1 |
| 总值 = 36 |
你留意表里的 对称 吗?
- 2 和 12 有相同个数的方法 = 1
- 3 和 11 有相同个数的方法 = 2
- 4 和 10 有相同个数的方法 = 3
- 5 和 9 有相同个数的方法 = 4
- 6 和 8 有相同个数的方法 = 5
掷 108 次
好,为什么要掷 108 次? 36 次不够给我们一个好结果。 360次当然很好,不过太费时了。 所以 108 次 ( 3 组,每组 36 次) 就差不多了。
把这些数字乘以三去符合 108 的总数:
| 总 得分 |
多少个 方法可以得到 这个分数 |
| 2 | 3 |
| 3 | 6 |
| 4 | 9 |
| 5 | 12 |
| 6 | 15 |
| 7 | 18 |
| 8 | 15 |
| 9 | 12 |
| 10 | 9 |
| 11 | 6 |
| 12 | 3 |
| 总值 = 108 |
这些是 理伦 值, 与你在 实验 得到的不一样。
理伦 值在柱状图上像这样:
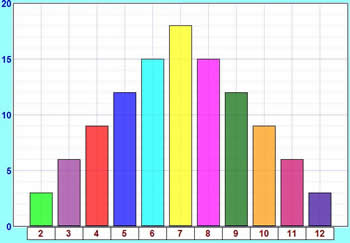
理论值和你的实验值比较起来怎么样?
这图和你的图应该相似, 但它们应该不会完全一样,因为你的实验有偶然性,同时你掷的次数亦相当小。
若你重复很多次这实验, 你的实验结果便会和理论相当接近。
我们已解答了当初开始实验时的问题:
最可能的得分是什么?
- 7 的柱子最高, 所以 7 是最可能的总得分。
这可能是为什么人们说 幸运的 7 。。。。。。 ?
概率
在 概率 页上有一个公式:
一起事项发生的概率 = 它可以发生的方法的数目 所有结果的数目
l例子: 2 的概率
有 36 个可能的结果.
只有 1 个方法可得到 2。
所以,得到 2 的概率是:
2 的概率 = 1 36
每个得分都做一次:
| 总 得分 |
概率 |
| 2 | 1/36 |
| 3 | 2/36 |
| 4 | 3/36 |
| 5 | 4/36 |
| 6 | 5/36 |
| 7 | 6/36 |
| 8 | 5/36 |
| 9 | 4/36 |
| 10 | 3/36 |
| 11 | 2/36 |
| 12 | 1/36 |
| 总和 = 1 |
所有概率的和是 1
任何实验:
所有 可能结果的概率的和是 1