活动：奥运田径赛道

当你看奥运赛跑比赛时，你有没有想过为什么运动员不在赛道的同一条线上起跑？

这叫“错列起跑”。

为什么要 错列起跑？

如果 他们在同一条线上起跑，在 外 赛道的运动员便要比在 内 赛道的运动员跑得远，因为在赛道上边和下边有部分是 半圆形 的。

因此，每条赛道都有一个特别的起跑点，好使每个比赛者都跑一样长的距离。

我们来学计算 400m 赛跑的正确起跑点

多远?

当运动员跑了一圈， 他跑了多远？

我们来看看 在 第一线（内线） 的运动员跑的路线。

规则是：如果第一线的边缘有边石，我们需要在离赛道内缘 0.3 m 的距离 （就是差不多运动员跑的地方）测量。 其他的赛道要离开 0.2 m。

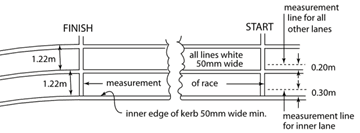
国际田联规则手册，规则 160.2

第一线赛道就像这样：

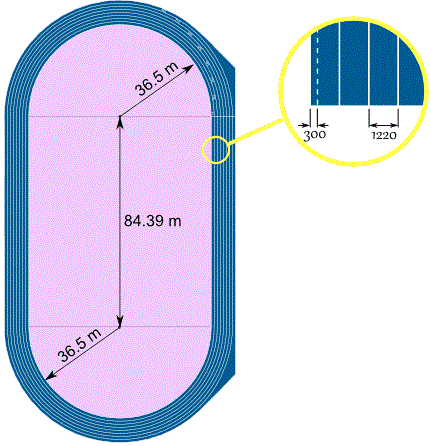
第一线赛道弯的部分的半径是 36.5 m，但我们要 加 0.3 m 去“跑的位置"，所以总长是 36.8 m

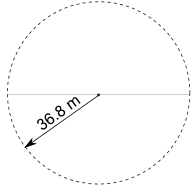两个弯的部分一起就是一个 半径 36.8m 的圆形。 看 圆形 这页来多了解些半径和圆周。

那么，要跑多远？答案：圆形的圆周加直线的部分。

那么巧！内线的长度正好是 400 m.

其实赛道的设计就是这样的。

第 2 线赛道呢？

每条赛道是 1220mm 宽，所以第二线的半径是 36.5 + 1.22 = 37.72 m

再 加 0.2 m 去到”跑的位置“ （第一线 0.3 m， 其他 0.2 m ），总长 37.92 m

这比 第一线长 7.04 m。。。。。。

。。。。。。所以第 2 线的起跑点应该在第 1 线 前 7.04 m 才公平

轮到你了

你可以完成以下的表吗？

赛道	半径	圆周	总 距离	错列起跑
1	36.8 m	231.22 m	400 m	0 m
2	37.92 m	238.26 m	407.04 m	7.04 m
3
4
5
6
7
8

 

你应该算出第 8 线的起跑线是在第 1 线的起跑线前面 53 米 ！

• 诧异吗？
• 公平吗?

这是公平的，因为错列起跑令到每个运动员都跑正好 400 米。

但有些人说， 在内线的运动员有优势，因为他们可以看到其他的跑手，从而知道怎样去追上去。

但也有人说在外线的运动员跑的弯道 没那么急。所以除非所有赛跑都在直的赛道比赛（像 100m 比赛），不然永远不会完全公平。

额外活动：面积

尝试计算 每条 赛道的面积（想像你要把它们涂上不同颜色）。

赛道的面积有圆的部分和直的部分。

 

我们不需要跑的位置，我们要知道 边缘的 半径。

 

第 1 线赛道内缘的半径是 36.5 m，所以第 1 线赛道外缘的半径（也是第 2 线赛道 内缘的半径)是 36.5 m + 1.22 m = 37.72 m

两个直的部分的面积 = 2 × 1.22 m × 84.39 m = 205.9 m² （算到小数点后一位）。

 

你来完成吧！ 每条赛道的面积会不同吗？ 一点不同，或者很大不同?

赛道	内缘 半径	外缘 半径	AIn = 内缘半径的圆形的面积	AOuy = 外缘半径的圆形的面积	AOut - AIn	两个直的部分的面积	赛道的总面积
1	36.5 m	37.72 m	4,185.4 m2	4,469.9 m2	284.5 m2	205.9 m2	490.4 m2
2	37.72 m
3
4
5
6
7
8