近似解
有时候求一个方程的精确解是很困难的。但是,可能一个近似解已经足够了!
什么是足够?
这在于你在做什么!
- 如果你在处理千百万的钱财,你应该做得非常精确,答案可能需要很多个有效数字。
- 但若你在计算派对需要多少食物,一个小小的误差就影响不大,你可以多买一点就稳妥了。
- 在这两个极端之间也可以!
所以明白你在做什么会帮你了解你需要的精确度。
解方程
以下可以帮助降低解方程时的误差:
- 先解 x = 某物
- 然后再计算
像这样:
例子:解 x/7 + 2π - 6.3068 = 0 (算到小数点后第三位)
| 开始: | x/7 + 2π - 6.3068 = 0 | |
| 把 2π - 6.3068 移到右边: | x/7 = - (2π - 6.3068) | |
| 乘以 7: | x = 7(6.3068 - 2π) | |
| 现在才计算: | x = 0.165 | |
为什么要等到最后才计算?因为每做一次计算,就会引入一些误差。若你多做几次计算,误差便会越累积越大。
检验
近似的答案只需要近似的检验
例子:检验 x = 0.165 是 x/7 + 2π - 6.3068 = 0 的解
| 把 0.165 代入 x: | 0.165/7 + 2π - 6.3068 = 0 | |
| 计算: | -0.00004 = 0 | |
不是绝对精确,但很近似。
图形估计
你可以用图形来找到不错的近似值,尤其当你使用放大功能时,像用我们的函数绘图器。
一个例子:
例子:估计 x3 - 2x2 - 1 = 0 的解(算到小数点后第三位)。
解法: 绘图!
这是我的第一次尝试。我看到线在大约 x=2.2 的位置穿过 y=0
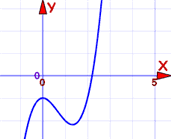
我们把它放大来仔细看交叉点:
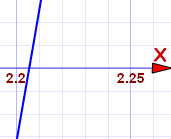
交叉点是在 2.20 与 2.21 之间……离2.21近一点。我们要小数点后两个位,所以答案是:
x3 - 2x2 - 1 = 0 的解是大约 x=2.21
检验: (2.21)3 - 2(2.21)2 + 2 = 大约 0.025,离 y=0 相当近