偶函数与奇函数
特别的函数
偶函数
函数是"偶函数",若然
f(x) = f(−x) ,x 为任何值,
换句话说,有沿y轴对称(像个镜面反射)的特性:
这是 f(x) = x2+1 的图
这些函数叫"偶"函数,因为 x2, x4, x6, x8 等函数都具有这个特性,但其他函数也会具有这种特性,例如 cos(x):
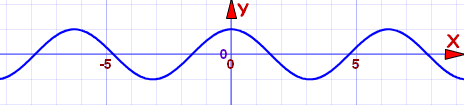
余弦函数: f(x) = cos(x)
它是个偶函数
可是一个偶指数不一定代表偶函数,例如 (x+1)2 就 不是偶函数。
函数是"奇函数",若然:
−f(x) = f(−x),x 为任何值,
留意 f 前面的负号: −f(x).
奇函数具有 原点对称的特性:
这是 f(x) = x3−x 的图
这些函数叫 "奇函数",因为 x, x3, x5, x7 等函数都具有这个特性,但其他函数也会具有这种特性,例如 sin(x):
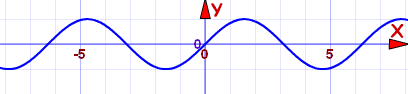
正弦函数: f(x) = sin(x)
它是个奇函数
可是一个奇指数不一定代表奇函数,例如 x3+1 就 不是奇函数。
非奇也非偶
不要被"奇" 和 "偶" 蒙了。。。。。。它们只不过是名称。。。。。。一个函数不一定是奇函数或偶函数。
实际上,大部分函数都既不是奇函数或偶函数。例如,只要把 1 加到以上的函数就得到这个:
这是 f(x) = x3−x+1 的图
它不是奇函数,也不是偶函数。
两个都不是!
偶还是奇?
例子:f(x) = x/(x2−1) 是偶函数、奇函数、或两个都不是?
把 −x 代入看看:
| 代入 "−x": | f(−x) | = (−x)/((−x)2−1) | |
| 简化: | = −x/(x2−1) | ||
| = −f(x) |
f(−x) = −f(x),所以它是奇函数
是偶也是奇
唯一是 偶函数,而且同时也是奇函数 的函数是 f(x) = 0
特别特性
加:
- 两个偶函数的和是偶函数。
- 两个奇函数的和是奇函数。
- 偶函数和奇函数的和不是偶函数,也不是奇函数(除非其中一个函数是零)。
乘:
- 两个偶函数的积是偶函数。
- 两个奇函数的积是偶函数。
- 偶函数和奇函数的积是奇函数。