介值定理

介值定理（又名中值定理）背后的概念是：

当连续的曲线连接着两点： 一点在直线下面 另一点在线上面 。。。。。。则曲线会在至少一个地方通过直线！

这还用说，当然要通过直线才能从A去到B！

介绍了理念后，我们来看细节。

连续

曲线一定要是连续的。。。。。。没有间断。

连续在微积分中是个专有名词，有精确的定义，但在这里我们用一个简单的定义：

比较正式一点

这是比较正式的描述：

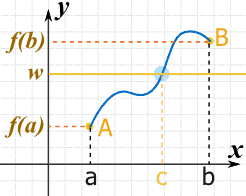		若： 曲线是函数 y = f(x)， 函数在区间[a, b] 里是连续的, 而 w是在 f(a) 与 f(b)之间的数，
		则。。。。。。

。。。。。。在 [a, b] 里至少有一个值 c，而使 f(c) = w

换句话说，函数 y = f(x) 在某一点一定符合 w = f(c)

注意：

• w 是在 f(a) 与 f(b) 之间， 这代表。。。。。。
• c 一定是在 a 与 b 之间

至少有一个 定理也说："至少有一个值 c"，就是说可能会有更多。 这例子有3点是 f(x)=w。

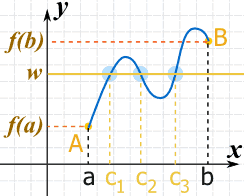有什么用？

每当我们知道：

• 线上面有一点
• 线下面有一点，并且
• 曲线是连续的，

我们便可以说： "中间有一点是刚好在线上"。

这个挺有趣

介值定理能修补不稳的桌子

若你的桌子因为地面不平而放不稳。。。。。。 。。。。。。你只需转转桌子就可以解决问题！ 但地面一定要是连续的（相当平滑）。

为什么这方法有效？

桌子一定会有三只脚在地上，和使桌子不稳的是第四只脚。

想象我们在转桌子，第四只脚插进地下了（假想是在沙滩上）：

• 第四只脚有时在地上，
• 有时在地下

所以在某一点它一定会刚好接触地面，而在这一点桌子就会放稳。

（著名的科学作家 Martin Gardner 在《科学美国人》曾经提及这个例子，文献里也有一个复杂的论证）。

再来一个

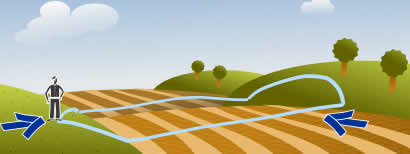
在一个往返的旅程里，你一定会
经过与起点是相同海拔的地方。

（但起点必须不是全程的最高点或最低点。）

理念是：

• 在旅途的某一点你的海拔会高于起点
• 在另一点你的海拔会低于起点

所以在这两点之间一定会有一点的海拔与起点是刚好相同的，但你的路程必须是连续的，你不能中途离开然后在另一点回来。

同样的道理也可以应用于温度、压力等等。

还有更多！

若你跟随一个圆形的路线。。。。。。在这圆形上会有些地方：

• 位置直接相对，
• 和海拔相同！

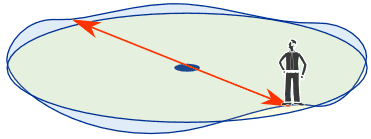
两点
直接相对和海拔相同