连续函数
连续函数的图是一条连续不断的线……
 ……你可以笔不离纸地把线画下来……
……你可以笔不离纸地把线画下来……
这不是个正式的定义,但可以帮你了解概念。
这是个连续函数:
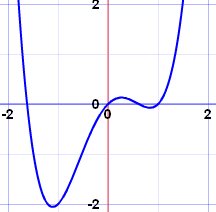
例子:
什么不是连续函数(也称 非连续函数)?
留意这些现象:缺口、间隙或垂直渐近线(函数向上或下趋向无穷大)。
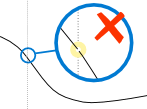 |
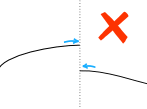 |
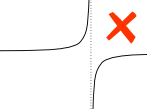 |
||
| 非连续 |
非连续 |
非连续 |
||
| (缺口) | (间隙) | (垂直渐近线) |
试试这些函数:
(用滑标可以放大/缩小、拖曳可以移位、点击可以置于中部。)
定义域
函数有个定义域。 定义域最简单的意思就是所有可以代入函数的值。 |
 |
根据定义域的不同,函数可以是连续或非连续!
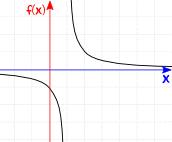
例子:1/(x-1)
在 x=1:
所以在 x=1 有个 "不连续点"
 |
 |
|
| f(x) = 1/(x-1) 对于全部 整数 |
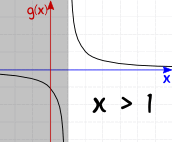
g(x) = 1/(x-1) 对于 x>1 | |
| 非连续 | 连续 |
g(x) 并不包括 x=1,所以它是连续的。
所以若函数在其定义域是连续的,它便是连续函数。
更正式的解释!
我们可以用 极限 来为 连续 下定义 (最好先去阅读该网页):
函数 f 是连续的,当:对于 每个 在其定义域的值,c:
f(c) 是 已定义的,并且:
![]()
"当 x 趋近 c 时,f(x) 的极限等于 f(c)"
极限的意思是:
"当 x 越来越趋近 c 时
f(x) 便越来越趋近 f(c)"
在每边趋近 c 都需要是这样:
| x (从左边)趋近 c f(x) 便趋近 f(c) |
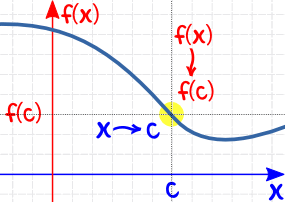 |
|
| 并且 x (从右边)趋近 c f(x) 便趋近 f(c) |
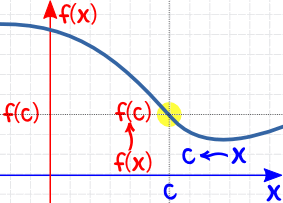 |
若从左边趋近的值和从右边趋近的值不同("间隙"),极限便不存在!
怎样使用:
对于所有 x 值,确保:
- f(x) 是已定义的
- 在 x 的极限等于 f(x)
举些例子:
例子:f(x) = (x2-1)/(x-1) 对于所有实数
函数在 x=1 时是未定义的:
(x2-1)/(x-1) = (12-1)/(1-1) = 0/0
所以 不是连续函数
我们来改变定义域:
例子:g(x) = (x2-1)/(x-1) 对于区间 x<1
差不多 是相同的函数,但定义域不包括 x=1。
所以它现在是个连续函数(不包括 "缺口")
例子:这个 分段函数 呢?
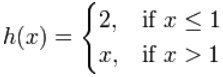 |
图像这样: | 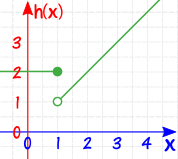 |
函数在 x=1 是已定义的,因为 h(1)=2 (没有 "缺口")
但在 x=1 你不能确定极限是多少,因为答案有两个可能:
- "2" (从左边),
- "1" (从右边)
实际上,极限在 x=1 并不存在(有个 "间隙")
因此,函数不是连续的。
可是:
例子:这个分段函数――绝对值
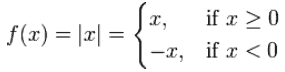 |
图象这样: | 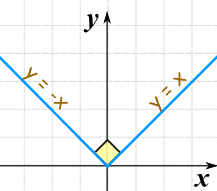 |
在 x=0 有一个尖锐的改变!
但函数在 x=0 仍然是已定义的,因为 f(0)=0 (没有 "缺口"),
趋近 x=0 的极限(从每边)都是 0 (没有 "间隙"),
所以函数是连续的。
(但函数不是 可微分的。)