分段函数
函数可以是分段的
我们可以建立在不同 （x）值有不同行为的函数。
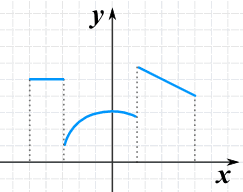
有 3个段的函数
例子：
- 若 x 小于 2，则返回 x2，
- 若 x 小于 2，则返回 6
- 若 x 大于 2 并且小于或等于 6，则返回直线 10-x
像这样：
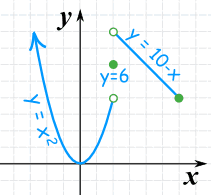
（实心圆点的意思是 "包括"，
空心圆点的意思是 "不包括"）
记法是：
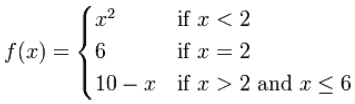
定义域（函数的所有输入值）是所有小于或等于 6的实数，可以写成：
Dom(f) = (-∞, 6] (using 区间符号)
Dom(f) = {x 
| x ≤ 6} (using 集合建构式符号)
这是一些数值：
| X | Y |
|---|---|
| -4 | 16 |
| -2 | 4 |
| 0 | 0 |
| 1 | 1 |
| 2 | 6 |
| 3 | 7 |
例子：这个也是分段函数：
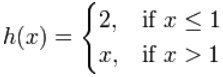
| 像这样： |  |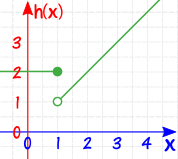
| h(-1) 是多少？ | x ≤ 1，所以用 h(x) = 2，h(-1) = 2 | |
| h(1) 是多少？ | x ≤ 1，所以用 h(x) = 2，h(1) = 2 | |
| h(4) 是多少？ | x > 1，所以用 h(x) = x，h(4) = 4 |
我么可以用分段函数来建立无所不能的函数！
例子：医生根据时间收费。
- 6分钟或以下的收费是 $50
- 6 到 15分钟的收费是 $80
- 15分钟以上的收费是 $80，另外 15分钟后每分钟 $5
可以写成这样：
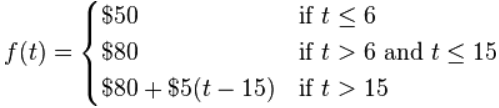
你看了 12分钟，收费是多少？$80
你看了 20分钟，收费是多少？$80+$5(20-15) = $105
绝对值函数
绝对值函数是个有名的分段函数。
它有两段：
- 零以下：-x
- 零及以上：x
f(x) = |x|
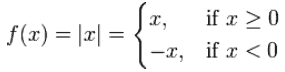
向下取整函数
向下取整函数是个很特别的分段函数，它有无穷多的段：
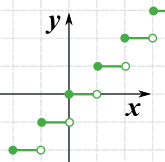
向下取整函数