集合建构式符号
怎样以成员的属性来描述集合。
 |
集合（简称：集）是由一个或多个确定的东西（通常是数字）所构成的整体。 例子：{5, 7, 11} 是个集合。 我们也可以用描述成员的方法来 "建立" 一个集合。 |
这是一个集合建构式符号的简单例子：
就是："所有 x 的集合，使得 x 大于 0"。
换句话说，任何大于 0 的值
注意：
- "x" 只不过是个位置标志符，可以用任何符号来代替，例如 { q | q > 0 }
- 有些人用 ":" 而不用 "|"：{ x : x > 0 }
数的种类
通常也会显示 x 是什么种类的数：
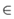的意思是 "的成员"（就是 "在"）
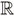是实数的独特符号。
所以意思是：
"所有实数的成员 x 的集合，
使得 x 大于或等于 3"
换句话说， "所有 3或以上的实数"
也有其它显示方法：
数的种类
我们在上面介绍了 （实数的特别符号）。以下是常见的数种类：
 |
 |
 |
 |
 |
 |
| 自然数 | 整数 | 有理数 | 实数 | 虚数 | 复数 |
例子：{ k 
| k > 5 }
"所有整数的成员 k 的集合，使得 k 大于 5"
换句话说，所有大于 5的整数。
也可以写成 {6, 7, 8, ... }，所以：
{ k | k > 5 } = {6, 7, 8, ... }
为什么要用集合建构式符号？
一个简单的集，例如 从 2 到 6 的整数 可以写成：
{2, 3, 4, 5, 6}
但怎样列出这个区间里的实数呢？
{2, 2.1, 2.01, 2.001, 2.0001, …… ？？？
所以我们写下怎样建立这个数列：
{ x | x ≥ 2 并且 x ≤ 6 }
在所有实数里限制只包括 2 到 6。
我们也可以在其它地方应用集合建构式符号：
{ x | x = x2 } = {0, 1}
所有实数 x，使得 x = x2
0 和 1 是唯一符合 x = x2 的实数
又一个例子
例子：x ≤ 2 或 x > 3
集合建构式符号像这样：
{ x | x ≤ 2 or x >3 }
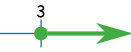
在实数直线上像这样：
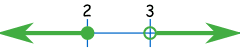
用区间符号是这样：
(-∞, 2] U (3, +∞)
我们用 "U" 来代表并集（两个集合的并合）。
定义域的定义
集合建构式符号是用来定义定义域的好方法。
简单地说，定义域是函数的所有输入值。
函数一定要在所有输入值上成立，所以我们要定义正确的定义域！
例子：1/x 的定义域
在 x=0，1/x 是未定义的（因为 1/0 是除以零）。
所以定义域不能包括 x=0：
1/x 的定义域是除了 0以外的所有实数
可以写成
Dom(1/x) = {x | x ≠ 0}
例子：g(x)=1/(x-1) 的定义域
在 x=1，1/(x-1) 是未定义的，所以要把 1 从定义域里剔除：
1/(x-1) 的定义域是除了 1 外的所有实数
用集合建构式符号来表达是：
Dom( g(x) ) = { x | x ≠ 1}
例子：f(x) = x/(x2 - 1) 的定义域
要避免除以零：x2 - 1 ≠ 0
分解3因子：x2 - 1 = (x-1)(x+1)
(x-1)(x+1) = 0 若 x = 1 或 x = -1，这是我们要避免的！
因此：
Dom( f(x) ) = {x | x ≠ 1, x ≠ -1}