集合入门
忘记了数字。
忘记了数字是什么。
以下讲的才是数学的源头。
不要管数字的数学,我们来看 "事物" 的数学。
定义
集合是什么?简单地说,集合是收集起来的一些东西。
我们先确定一堆 "东西"(下面会有定义)的一个共同属性,然后我们收集有这个共同属性的 "东西" 。

例如,穿在身上的东西:鞋子、袜子、帽子、衬衫、裤子等等。
你很容易就可以想到很多其他的集合。
这就是个集合。
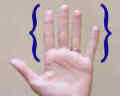
另一个例子是手指。 这个集合含有食指、中指、无名指和小指。 |
 |
集合只不过是一推有共同属性的东西。
记法
集合的记法相当简单。把所有元素(也称 "成员")以逗号分隔,放在大括號里:
大括号{ } 有时也叫做 "花括号"。
这是上面的两个例子:
{袜子,鞋子,手表、衬衫 …}
{食指,中指,无名指,小指}
第一个例子有这个符号 "…"(三个圆点)。
这三个圆点… 叫水平省略号,意思是 "延续下去"。
所以第一个例子的意思是无穷延续 … 。
(你可能说其实没有无穷的东西可以穿在身上,但这也很难说 …… 在是个例子我们就当作真是无穷的。)
所以:
- 第一个集 {袜子,鞋子,腕表,衬衫,…} 叫无限集合,
- 第二个集 {食指,中指,无名指,小指} 叫 有限集合.
但有时 "…" 可以使用在一个长系列的成员中间:
例子:英语字母集合:
{a, b, c, …, x, y, z}
这个例子是个有限集合(只有 26个英语字母)
数集
这和数学有什么关系?为集合定义需要一个共同的属性,我们也可以这样定义数的集合.
奇数集:{..., -3, -1, 1, 3, ...}
质数集:{2, 3, 5, 7, 11, 13, 17, ...}
小于 10 的 3 的正倍数:{3, 6, 9}
还有很多。
数集(其实所有的集都一样)也可以没有共同的属性,我们只需要把一些东西定义为一个集合。例如:
{4, 5, 6, 10, 21}
{2, 949, 48282, 42882959, 119484203}
这些都是我在键盘上随意打出来的数。
集合为什么重要?
集合是数学的基本概念。集合的概念没有什么特别,但应用在不同的(数学)情况下则成为强大的数学基础工具。
数学可以是很复杂的学问。图论、抽象代数、实分析、复分析、线性代数、数论等等都是复杂的理论,但它们其中一个共同基础就是集合。
全集
 |
在上面我们说:"东西"。 这个集合叫全集。它是包含所有的集合。在实际的层面,全集含有所有与当前的研究课题有关的东西。 |
|
 |
研究整数时,相关的集合都含有整数。全集就是所有整数。 在数论研究,全集多半是所有整数,因为数论就是整数的研究。 |
|
 |
在复分析里,全集就是复数。 |
更多记法
 |
我们通常用大写英语字母来代表集合,小写子母来代表集合的元素。 例如,A 是个集合,a 是 A 的一个元素。B 与 b 和 C 与 c 也是一样。 |
当然,你不一定需要永远跟随这个惯例,你可以用 m 来代表集合,这并不违背数学定律(但是,除以 0 就是犯(数学)法的行为,你会被打进数学大牢里监禁π年)。不过,这个惯例也很清晰简单,所以跟随它也没什么大不了。
如果我们能说 a 是 A 集的元素,我们就用 ![]() 符号来表示。
符号来表示。
"不是集的元素"也有个符号:![]() 。
。
例子:集 A 是 {1,2,3}。我们可以这样写 1 ![]() A,但 5
A,但 5 ![]() A
A
相等
如果两个集合所有的成员都是相同的,它们便是相等的。但是,有时两个相同的集合乍看是不相等的,所有我们需要小心观察!
例子:A 与 B 相等吗?
- A 是头四个正整数的集
- B = {4, 2, 1, 3}
我们检测一下。两个集都含有 1。也有 2、3 和 4。没有其他元素了。所以:是,这两个集是相同的!
相等的符号是等号(=),所以:
A = B
子集
一个集合的一部分就是它的子集。
例子:集 {1, 2, 3, 4, 5}
其中一个子集是 {1, 2, 3}。{3, 4} 或 {1} 也是子集。
但 {1, 6} 不是子集,因为 6 不是原集的元素。
一般来说:
A 是 B 的子集当且仅当 A 的每个元素都是 B 的元素。
我们来看一些例子。
例子:A 是不是 B 的子集?A = {1, 3, 4},B = {1, 4, 3, 2}。
1 是 A 的元素,也是 B 的元素。
3 是 A 的元素,也是 B 的元素。
4 是 A 的元素,也是 B 的元素。
A 没有其他元素了,所有 A 的元素都是 B 的元素,所以
A 是 B 的子集
注意 2 是 B 的元素,但不是 A 的元素。但这没关系,我们只看 A 的元素。
现在我们来看一个比较复杂的例子。
例子:A 是 4 的所有倍数,B 是所有 2 的倍数。A 是 B 的子集吗?B 是 A 的子集吗?
我们不能检测所有的元素,因为两个集都是无限集。所以我们要做些分析。
集合是:
- A = {…, -8, -4, 0, 4, 8, …}
- B = {…, -8, -6, -4, -2, 0, 2, 4, 6, 8, …}
把两个集的元素配对,我们知道每个 A 的元素都是 B 的元素,但 B 的元素不一定是 A 的元素:
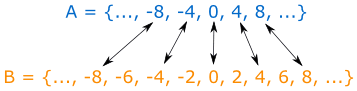
因此:
A 是 B 的子集,但 B 不是 A 的子集
真子集
子集的定义导致一个有趣的结论。
A 是个集。每个 A 的元素都是 A 的元素吗?(很奇怪的问题,写错了吗?)
没写错,答案:当然是!
所以 A 是 A 的子集。
A 不像是自己真的子集。通常我们要真正的子集。所以我们建立另一个概念:真子集。
A 是 B 的真子集当且仅当每个 A 的元素也是 B 的元素,并且至少有一个 B 的元素不是 A 的元素。
在这个定义里,第二个条件排除了 A 为自己的真子集的可能。除此之外,真子和子集是没有分别的。
例子:
{1, 2, 3} 是 {1, 2, 3} 的子集,但不是 {1, 2, 3} 的 真子集。
例子:
{1, 2, 3} 是 {1, 2, 3, 4} 的真子集,因为 4 不在第一个集里。
注意如果 A 是 B 的真子集,它也是 B 的子集。
更多更多记法
如果 A 是 B 的子集,我们这样写:A ![]() B。
B。
如果 A 不是 B 的子集,我们这样写:A ![]() B ("A 不是 B 的子集")
B ("A 不是 B 的子集")
如果 A 是 B 的真子集,我们拿走符号下面的横线:A ![]() B,如果不是子集(也不是真子集):A
B,如果不是子集(也不是真子集):A ![]() B。
B。
空集(也称零集)
很奇怪的概念!

想象这个集合:吉他的钢琴键。
"荒谬!""吉他没有钢琴键!"
全对!这个集没有元素。
这个集合叫空集(或零集)。它没有任何元素。一个都都没有。零个。
符号是![]()
或这个符号:{}(没有元素的集合)
另一个空集的例子是地球上南极以南的国家。
空集有什么奇怪?继续看下去!
空集与子集
我们再来看子集的定义。有一个集 A。可以是任何集。空集是 A 的子集吗?
根据是子集的定义:若空集的每个元素都是 A 的元素,则空集是 A 的子集。但是,空集是没有元素的!
这个陈述是 "空虚"的真(也叫 "琐碎"的真)的。这是一个逻辑学的课题。
你可以这样想:我们找不到任何不在集 A 里的空集的元素,所以空集的所有元素都在 A 里。
因此空集是 A 的子集。
空集是任何集的子集,包括空集自己。
势
在集合里,元素的次序是无关重要的。
例子:{1,2,3,4} 和 {3,1,4,2} 是同一个集合
集合的 "势" 就是集合的大小。
有有限集和无限集,也有有穷势和无穷势。
有限集的势是元素的个数。
例子:{10, 20, 30, 40} 的势是 4。
无限集的势是无穷大。在集合论里,无穷大也有大小之分,但这是个比较高级的课题。
还有记法!
不,没有了。不再讲记法了。
| 作者:
Ricky Shadrach |