活动:子集
请先阅读 集合入门 !
这活动探讨 一个集合有多少个 子集。
什么是子集?
子集 是在一个 集合里面 的集合
比方,你可以从下面的口味选择冰淇淋:
你可以选一个口味 (香蕉)、 (巧克力),或 (香草),
或两种口味 {香蕉、巧克力}、 {香蕉、香草} 或 {巧克力、香草},
或全部三种口味都选(这不算贪心),
或者 你什么都不选,"不要了,谢谢",这就是选 "空集":{}
例子:集合 {小李、小王、小明、波波}
有以下的子集:
- {小李}
- {小王}
- ……
也有这些子集:
- {小李、小王}
- {小李、小明}
- {小王、波波}
- ……
还有:
- {小李、小王、小明}
- {小李、小王、波波}
- ……
和
- 全集: {小李、小王、小明、波波}
- 空集: {}
我们从空集开始:
空集
空集有多少个子集?
你可以选:
- 全集: {}
- 空集: {}
但在这情况下它们是同一样的东西!
所以 空集只有 1 个子集 (就是 它自己,空集)。
就好像问你:“什么都么没有,你选什么?”,答案是: “什么都不选”。 是你唯一的选择。 完了。
有 一个元素的集合
可以是任何一个集合,我们用:
{苹果}
集合 {苹果} 有多少个 子集 ?
- 全集: {苹果}
- 空集: {}
就是这么多。你可也选一个元素,或什么都不选。
所以有 一个 元素的集合有 2 个子集。
有 两个元素的集
我们加一个元素:
{苹果、香蕉}
这个集合 {苹果、香蕉} 有多少个子集?
有 {苹果}或 {香蕉},和:
- 全集 {苹果、香蕉}
- 空集 {}
所以有 两个 元素的集合有 4 个子集。
有 三个元素的集
这个呢?
{苹果、香蕉、樱桃}
我们要有系统的来做,把子集和元素逐一列出来:
一个元素: {苹果}、 {香蕉}、 {樱桃}
两个元素: {苹果、香蕉}、 {苹果、樱桃}、 {香蕉、樱桃}
和:
- 全集: {苹果、香蕉、樱桃}
- 空集: {}
做一个列表:
| 列 | 子集 数目 |
|
| 零个元素 | {} | 1 |
| 一个元素 | {苹果}、{香蕉}、{樱桃} | 3 |
| 两个元素 | {苹果、香蕉}、{苹果、樱桃}、{香蕉、樱桃} | 3 |
| 三个元素 | {苹果、香蕉、樱桃} | 1 |
| Total: | 8 | |
(注意: 看到规律吗?)
有 四个元素的集合(你来做)
用这个集合来做:
{苹果、香蕉、樱桃、枣}
用以下列表:
| 列 | 子集 数量 |
|
| 零个元素 | {} | |
| 一个元素 | ||
| 两个元素 | ||
| 三个元素 | ||
| 四个元素 | ||
| 总计: | ||
(注意: 若你做得对,数字会有个规律。)
有 五个元素的集合
现在来做这个:
{苹果、香蕉、樱桃、枣、蛋}
用以下列表:
| List列 | 子集 数量 |
|
| 零个元素 | {} | |
| 一个元素 | ||
| 两个元素 | ||
| 三个元素 | ||
| 四个元素 | ||
| 五个元素 | ||
| 总计 | ||
(数字有规律吗?)
有 六个元素的集零元素
来这个:
{苹果、香蕉、樱桃、枣、蛋、巧克力糖浆}
够了……我们不用填列表了, 因为
加倍
首先注意到的是子集的数目每次加倍:
有 n 个元素的集有 2n 子集
你应该知道:
- 有六个元素的集合有多少个子集? _____
- 有七个元素的集合有多少个子集? _____
另一个 规律
现在来想想 子集和大小:
- 空集 只 有 1 个子集: 1
- 有一个元素的集合 有一个 没有元素的子集和 1 个有一个元素的子集 : 1 1
- 有两个元素的集合 有 1 个没有元素的 子集, 2 个有一个元素的 子集和 1 个有两个元素的 子集: 1 2 1
- 有三个元素的集 有 1 个没有元素的 子集, 3 个 有一个元素的 子集, 3 个 有两个元素的子集和 1 个 有三个元素的 子集: 1 3 3 1
- 依此类推!
看到 数字的规律吗?
这些是 杨辉三角里的数字!
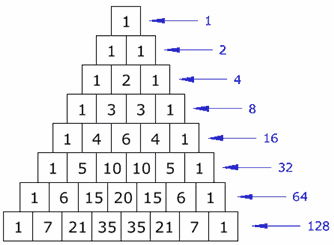
这 很有用,因为你可以查验你的子集数目是不是对的。
注意: 行从 0 开始,列也是。
例子: 集合 {苹果、香蕉、樱桃、枣、蛋} 有这些有三个元素的子集:
- {苹果、香蕉、樱桃}
- {苹果、香蕉、枣}
- {苹果、香蕉、蛋}
- {苹果、樱桃、蛋}
但这只是 4 个子集,应该总共有几个?
你从 5 个选 3 个,所以去 杨辉三角 的第 5 行,第 3 位置(记得从 0 开始),你知到有 10 个子集。再想想!
答案是: {苹果、香蕉、樱桃} {苹果、香蕉、枣} {苹果、香蕉、蛋} {苹果、樱桃、枣} {苹果、樱桃、蛋} {苹果、枣、蛋} {香蕉、樱桃、枣} {香蕉、樱桃、蛋} {香蕉、枣、蛋} {樱桃、枣、蛋}
计算数字
有计算这些数字 1、4、6、4 和 1 的方法吗 (除了用杨辉三角外)?
有。我们可以用 组合 来计算 有多少个 选每个数目的元素 的方法。
集合里有四个元素,同时:
- 从 4 个元素选 0 个的方法的数目是 = 4C0 = 1
- 从 4 个元素选 1 个 的方法的数目是 = 4C1 = 4
- 从 4 个元素选 2 个的方法的数目是 = 4C2 = 6
- 从 4 个元素选 3 个的方法的数目是 = 4C3 = 4
- 从 4 个元素选 4 个的方法的数目是 = 4C4 =1
- 子集的 总数 = 16
用有五个元素的集合来试试。
完成以下:
- 从 5 个元素选 0 个 的方法的数目是 = 5C0 = 1
- 从 5 个元素选 1 个 的方法的数目是 = ___________
- 从 5 个元素选 2 个的方法的数目是 = ___________
- 从 5 个元素选 3 个的方法的数目是 = ___________
- 从 5 个元素选 4 个的方法的数目是 = ___________
- 从 5 个元素选 5 个的方法的数目是 = ___________
- 子集的总数 = ___________
结论
在这活动里你:
- 发现了一条规则去 计算一个集合有多少个子集:有 n 个元素的集 有 2n 个子集。
- 看到 不同大小的集合的子集的数目与 杨辉三角的关系。
- 发现一个用组合来快捷 计算这些数目的方法。
更为 重要的是,你看到不同的数学分枝可以怎样 结合在一起.