杨辉三角
|
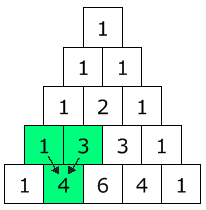
要想画杨辉三角,先把 "1" 方在顶点,然后连续在下面按三角形的模式放上数字。 每个数是它上面两个数的和。 (这里我突出了 1+3 = 4) |
 |
杨辉三角里面的规率
对角线
第一条对角线全是 "1"
下一条对角线是 正整数 (1、2、3、等等)
第三条对角线是 三角形数
(第四条对角线是 四面体数。)

对称
杨辉三角也是 对称的,左边的数在右边重复,像个镜像。
每行的和
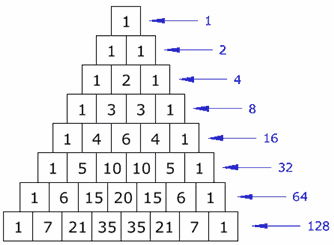
每行的和有什么特别?
有规率吗?
每行的和是上一行的和的 两倍 (2 次方 )。
11的乘方
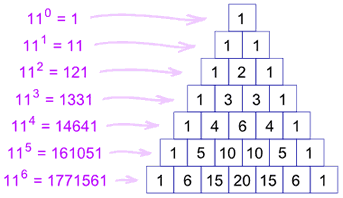
每行是 11 的 (乘方):
- 110=1 (第一行是 "1")
- 111=11 (第二行是 "1" 和 "1")
- 112=121 (第三行是 "1"、"2"、"1")
- 等等!
那 115 呢? 简单! 把数字重叠起来,像这样:
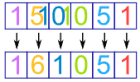
依此类推,116,等等。
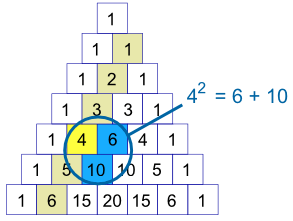 |
平方在第二条对角线,每个数的平方等于右边的数和它们下面的数的和。 例子:
|
这是有理由的。。。。。。你来想想。 (提示: 42=6+10, 6=3+2+1, and 10=4+3+2+1)
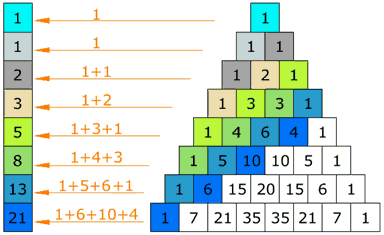
斐波那契数列
试试这个: 先选一行最左边的 1,然后选向上一步再向右一步的数,重复这个步骤直到没有可选的数字。把这样选的数加起来(如图)。。。。。。你会得到 斐波那契数列。
(斐波那契数列 从 "0, 1" 开始,然后把连续的两个数的和作为数列的下一个数,例如 3+5=8,然后 5+8=13,依此类推等)
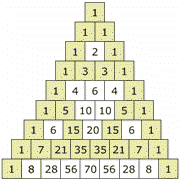
单数和双数
若你把单数和双数涂上不同颜色,你会得到 谢尔宾斯基三角形的图案
杨辉三角的应用
正面和反面
杨辉三角能显示抛硬币时不同的结果组合,从而得到任何结果组合的 概率。
例如,若你抛三次硬币,只有一个有三个正面的组合(HHH),但有三个有两个正面和一个反面的组合(HHT、HTH、THH),也有三个有一个正面和两个反面的组合(HTT、THT、TTH),一个全是反面的组合(TTT)。这就是杨辉三角里的 "1、3、3、1" 模式。
| 抛硬币次数 | 可能结果(分组) | 杨辉三角 |
|---|---|---|
| 1 | H T |
1, 1 |
| 2 |
HH HT TH TT |
1, 2, 1 |
| 3 |
HHH HHT, HTH, THH HTT, THT, TTH TTT |
1, 3, 3, 1 |
| 4 |
HHHH HHHT, HHTH, HTHH, THHH HHTT, HTHT, HTTH, THHT, THTH, TTHH HTTT, THTT, TTHT, TTTH TTTT |
1, 4, 6, 4, 1 |
| ... etc ... |
例子: 抛四次硬币,得到两个正面向上的概率是多少?
总共有 1+4+6+4+1 = 16 (或 24=16)个可能结果,其中 6 个有两个正面。所以概率是 6/16,或 37.5%
组合
杨辉三角也显示物品可能 组合 的数量。
例子: 有 16 个台球,有几个不同的方法去选 3 个(不管次序)?
答案:去第 16 行 (顶行是 0),第 3 个 (最左是 0)的值就是答案:560。
这是第 16 行附近:
1 14 91 364 ... 1 15 105 455 1365 ... 1 16 120 560 1820 4368 ...
杨辉三角里任何数的公式
在组合学 里有一条杨辉三角里任何数的公式:
通常称为 "n 取 k",这样写: |
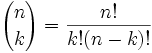 |
标志法:"n 取 k" 也可以写成 C(n,k), nCk 或 nCk 或 Cnk。
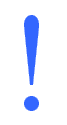 |
"!" 代表 "阶乘",意思是一列逐渐减小的整数的积。 例子:
|
所以杨辉三角也可以是 (注意:顶行是 行 0 |
 |
例子:杨辉三角里 行 4,数 2 是 "6" ...
。。。。。。我们来看看公式是不是对的:
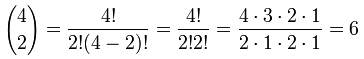
是对的!你自己来试试。
这很有用。。。。。。你可以用这个公式 直接 计算杨辉三角里任何的数,而不用先计算它上面的数。
多项式
杨辉三角也可显示 二项展开式的系数:
| 幂 | 二项展开式 | 杨辉三角 |
|---|---|---|
| 2 | (x + 1)2 = 1x2 + 2x + 1 | 1, 2, 1 |
| 3 | (x + 1)3 = 1x3 + 3x2 + 3x + 1 | 1, 3, 3, 1 |
| 4 | (x + 1)4 = 1x4 + 4x3 + 6x2 + 4x + 1 | 1, 4, 6, 4, 1 |
| ... etc ... |
头 15 行
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1
1 11 55 165 330 462 462 330 165 55 11 1
1 12 66 220 495 792 924 792 495 220 66 12 1
1 13 78 286 715 1287 1716 1716 1287 715 286 78 13 1
1 14 91 364 1001 2002 3003 3432 3003 2002 1001 364 91 14 1
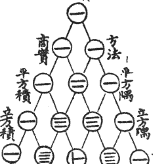 |
中国对杨辉三角的认知这个图叫"古法七乘方图"。放大 记载于朱世杰在公元1303年(700 多年前)写的 《四元玉鉴》的前页,比欧洲最先谈及这个三角形的法国数学家帕斯卡早三百年。 并且书中说明此表引自11世纪中(约公元1050年)贾宪的《释锁算术》。而在南宋时期,在杨辉1261年所著的《详解九章算法》一书中,也辑录了这个三角形数表。 |
梅花机 (英语:"The Quincunx")
 |
法兰西斯・高尔登所发明的一个巧妙的小机器。它是个用木钉制成的杨辉三角,名为 "The Quincunx" (梅花机). 向第一个森钉投下球,然后自己掉到三角形底部的小箱子里。
|