斐波那契数列
斐波那契数列是这样的数列:
0、1、1、2、3、5, 8、13、21、34 ……
下一项是上两项的和。
- 2 是上两项的和(1+1)
- 3 是上两项的和(1+2)、
- 5 是(2+3)、
- 依此类推!
例子:下一项是 21+34 = 55
就是这么简单!
长一点的斐波那契数列:
0、1、1、2、3、5、8、13、21、34、55、89、144、233、377、610、987、1597、2584、4181、6765、10946、17711、28657、46368、75025、121393、196418、317811 ……
你可以计算后面几项吗?
做个螺旋
用这些数作为边长来画正方形,就得到漂亮的螺旋图象:
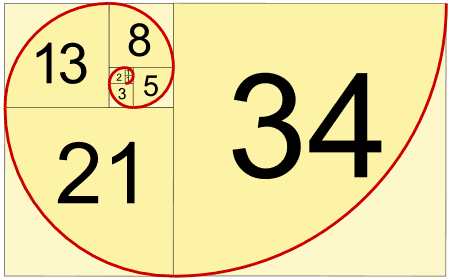
留意正方形整齐地形成螺旋形。
例如,5 和 8 是 13、8 和 13 是 21 等等。
规律
斐波那契数列可以用一个 "规律" 来表达(见数列与级数)。
我们先把项从 0 开始排列:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | …… |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | …… |
第 6 项的符号是 x6 (等于 8)。
例子:第8项是
|
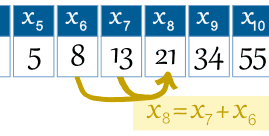 |
所以可以这样写成规律:
规律是 xn = xn-1 + xn-2
其中:
- xn 是第 "n" 项
- xn-1 是上一项(n-1)
- xn-2 是再上一项(n-2)
例子:这样计算第 9 项:
| x9 | = x9-1 + x9-2 |
| = x8 + x7 | |
| = 21 + 13 | |
| = 34 |
黄金比例
奇妙的事:两个连续的斐波那契数的比非常接近黄金比例,"φ",大约是 1.618034……
两个连续的斐波那契数越大,它们的比就越接近黄金比例:
|
A |
B |
B / A |
|
|---|---|---|---|
|
2 |
3 |
1.5 | |
|
3 |
5 |
1.666666666…… | |
|
5 |
8 |
1.6 | |
|
8 |
13 |
1.625 | |
|
…… |
…… |
…… | |
|
144 |
233 |
1.618055556…… | |
|
233 |
377 |
1.618025751…… | |
|
…… |
…… |
…… |
注意:我们可以随机选两个正整数做为数列的开始,这个比例也是成立的。例如我们可以用 192 和 16 来开始建立数列:192、16、208、224、432、656、1088、1744、2832、4576、7408、11984、19392、31376 ……:
| A |
B |
B / A |
|
|---|---|---|---|
192 |
16 |
0.08333333…… | |
16 |
208 |
13 | |
208 |
224 |
1.07692308…… | |
224 |
432 |
1.92857143…… | |
…… |
…… |
…… | |
7408 |
11984 |
1.61771058…… | |
11984 |
19392 |
1.61815754…… | |
…… |
…… |
…… |
虽然需要多几项才能得到好的比,但这显示了不一定要斐波那契数列才有这个属性!
用黄金比例来计算斐波那契数
更奇妙的是,我们可以用黄金比例来计算任何斐波那契数:
![]()
答案一定是个正整数,刚好等于上两项的和。
例子:
![]()
用计算器来算(黄金比例只输入到六位小数),返回的答案是 8.00000033。更精确计算的答案会更接近 8。
自己去试试看!
趣事
这是斐波那契数列:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | …… |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | 610 | …… |
这是个有趣的规律:
- 留意 x3 = 2。每 3个数是 2 的倍数(2、8、34、144、610 ……)
- 留意 x4 = 3。每 4个数是 3 的倍数(3、21、144 ……)
- 留意 x5 = 5。每 5个数是 5 的倍数(5, 55, 610 ……)
依此类推。(每 n个数是 xn 的倍数)。
1/89 = 0.011235955056179775……
留意头几个小数位(0、1、1、2、3、5)就是斐波那契数列。
其实所有的小数位都是,不过多于一个数位的数(13、21 等等)是重叠的,像这样:
| 0.0 |
| 0.01 |
| 0.001 |
| 0.0002 |
| 0.00003 |
| 0.000005 |
| 0.0000008 |
| 0.00000013 |
| 0.000000021 |
| …… 等等 …… |
| 0.011235955056179775…… = 1/89 |
小于零
数列在零以下也一样:
| n = | …… | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | ... |
| xn = | …… | -8 | 5 | -3 | 2 | -1 | 1 | 0 | 1 | 1 | 2 | 3 | 5 | 8 | …… |
(自己来算算,看看每项是不是上两项的和!)
在零以下,斐波那契数和在零以上一样,不过正负号跟随+-+- 的规律。公式可以这样写:
x−n = (−1)n+1 xn
就是说:第 "-n" 项等于 (−1)n+1 乘以第 "n" 项,(−1)n+1 的规律就是 1、-1、1、-1 ……
历史
斐波那契不是第一个发现这数列的人,很久以前印度已经知道这个数列了!

斐波那契
斐波那契的真名是比萨的列奧纳多,公元 1170 到 1250 活于意大利。
"斐波那契" 是别名,意思是 "波那契的儿子"。
除了斐波那契数列以外,他也在欧洲广泛推广使用阿拉伯数字(就像我们想在用的数字 0、1、2、3、4、5、6、7、8、9)来代替罗马数字(I、II、III、IV、V 等等)。这样以后写数字就简单多了!谢谢,列奧纳多。

斐波那契日
十一月二十三日是斐波那契日,因为 "1, 1, 2, 3" 是斐波那契数列的头几个数。在十一月二十三日记得告诉你的朋友!