常见数型
一组数可以有巧妙的形式。
以下是最常见的形式和它们的规律。
等差数列 (算术数列)
等差数列 的规律是每次 加 相同的值(常数)。
例子:
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
在这个数列里,数与数之间的差是 3。
延续下去,每次在前一项的基础上加3,像这样:

例子:
| 3, 8, 13, 18, 23, 28, 33, 38, ... |
在这个数列里,数与数之间的差是 5。
延续下去,每次向前一项加5,像这样:

每次加的值叫 "公差"
在这个例子里,公差是什么?
| 19, 27, 35, 43, ... |
答案: The common difference is 8
例子:
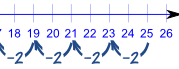
| 25, 23, 21, 19, 17, 15, ... |
公差是 −2
数列以每次 减 2 来延续,像这样:
 |
等比数列 (几何数列) 的规律是每次 乘 相同的值。
等比数列 的规律是每次 乘 相同的值。
例子:
| 1, 3, 9, 27, 81, 243, ... |
在这数列里,数与数之间的因数是 3.
数列以每次 乘 3 来延续,像这样:
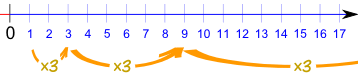
每次乘的值叫 "公比".
上面的例子的公比是 3:
可以用任何一个数开始:
例子:公比 3,但从 2 开始
| 2, 6, 18, 54, 162, 486, ... |
这数列的公比也是3,但从2开始。

例子:
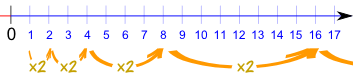
| 1, 2, 4, 8, 16, 32, 64, 128, 256, ... |
这数列从 1 开始,公比是 2。
数列以每次乘 2 来延续,像这样:
例子:
| 10, 5, 2.5, 1.25, 0.625, 0.3125, ... |
这世俗列从 10 开始,公比是 0.5 (一半)。
数列以每次乘 0.5来延续。
但公比不能是 0,否则数列就像这样: 1,0,0,0,0,0,0。。。。。。
特别数列
三角数
| 1, 3, 6, 10, 15, 21, 28, 36, 45, ... |
三角数列 是从一组按三角形图案排列的点所形成。
添加一行点,然后数所有的点,就是数列的下一项:

平方数
| 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
平方数是整数的平方:
0 (=0×0)
1 (=1×1)
4 (=2×2)
9 (=3×3)
16 (=4×4)
等等。。。。。。
立方数
| 1, 8, 27, 64, 125, 216, 343, 512, 729, ... |
立方数是整数的立方 (从 1 开始):
1 (=1×1×1)
8 (=2×2×2)
27 (=3×3×3)
64 (=4×4×4)
等等。。。。。。
斐波那契数
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... |
斐波那契数列 的规律是是把前两项加起来为下一项。
2 是前两项的和 (1+1)
21 是前两项的和 (8+13)
下一项是 55 (21+34)
你可计算下几项吗?
其他数列
还有很多!你甚至可以自己创造。。。。。。
