等比数列及它的和
数列
序列是一组顺序排列的东西,若这些东西是数,我们便称之为数列。
等比数列
在等比数列里,每一项和下一项的比是个常数。
例子:
| 2,4,8,16,32,64,128,256……/font> |
每项和下一项的比是 2。
除了第一项外,每项是上一项乘以2。
等比数列的一般写法是:
{a,ar,ar2,ar3…… }
其中:
- a 是首项,
- r 是项与项之间的比 (叫 "公比")
例子: {1,2,4,8……}
这个数列从 1 开始,然后每项加倍,所以
- a=1 (首项)
- r=2 ("公比":每项加倍)
数列是:
{a,ar,ar2,ar3…… }
= {1,1×2,1×22,1×23, ...…… }
= {1,2,4,8…… }
但留意,r 不能是 0:
- 若 r=0,数列便是 {a,0,0……},不是等比数列了
规则
我们可以用以下的规则来求任何一项:
xn = ar(n-1)
(用 "n-1",因为首项是 ar0)
例子:
| 10,30,90,270,810,2430,…… |
每项和下一项的比是 3。
a 和 r 是:
- a = 10 (首项)
- r = 3 ("公比")
规则是:
xn = 10 × 3(n-1)
所以,第 4 项是:
x4 = 10×3(4-1) = 10×33 = 10×27 = 270
第 10 项是:
x10 = 10×3(10-1) = 10×39 = 10×19683 = 196830
等比数列也可以有越来越小的项:
例子:
| 4,2,1,0.5,0.25…… |
每项和下一项的差是 0.5(一半)。
规则是 xn = 4 × (0.5)n-1
"几何"数列
等比数列也叫"几何数列"。为什么?因为数列好像几何维数的扩大:
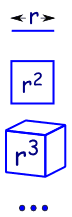 |
一条线是 1 维,长度是 r |
| 平方型是 2 维,面积是 r2 | |
| 正方体型是 3 维,体积是 r3 | |
| 。。。等。。。(在数学里可以有 4 维或更高)。 |
等比数列的和:等比级数
我们用以下的公式把等比数列的项加起来。
加:
a + ar + ar2 + ... + ar(n-1)
每项是 ark,k 从 0 开始,到 n-1 为止
公式是:
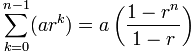
a 是首项
r 是项与项之间的 "公比"
n 是项的个数
使用公式很简单……只需 "代入" a、r 和 n 的值
例子: 把以下的等比数列的头 4 项加起来
| 10、30、90、270、810、2430…… |
每项和下一项的比差是 3。
a、r 和 n 是:
- a = 10(首项)
- r = 3("公比")
- n = 4(加头 4 项)
所以:
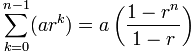
变成:
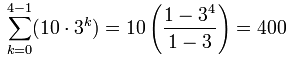
自己来检验:
10 + 30 + 90 + 270 = 400
在这例子,把它加起来就可以,以为只有 4 项。但如果有 50 项……用公式就方便多了。
使用公式
让我们来看看怎样使用这个公式:
例子:棋盘上的米
在二进制数字这页,我们提及棋盘上的米的例子。问题是:
把米这样放到棋盘上:
- 1 颗米在第一个格子,
- 2 颗米在第二个格子,
- 4 颗米在第三个格子,
- 依此类推……
……每个格子里的米是上一个格子的 两倍……
……棋盘上总共有多少颗米?
已知:
- a = 1(首项))
- r = 2(每项大一倍)
- n = 64(棋盘有 64 个格子)
所以:
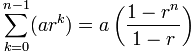
变成:
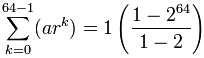
= (1-264) / (-1) = 264 - 1
= 18,446,744,073,709,551,615
和在 二进制数字 这页算出来的一样。(真巧!)
再举个例,这次 r 小于 1:
例子:把以下的等比数列的头 10 项加起来(每项是上一项的一半):
{ 1/2,1/4,1/8,1/16……}
a、r 和 n 是:
- a = ½(首项)
- r = ½(每次小一半)
- n = 10(加 10 项)
所以:
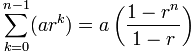
变成:
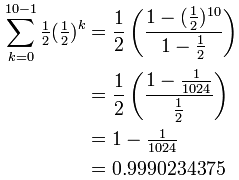
离 1 很近。
(问题:n 越来越大会怎样?)
为什么公式是这样的?
我们来看看为什么公式是这样的,我们会用一个有趣的"技巧"。
| 首先,以 "S"为数列的和: | S = | a + ar + ar2 + …… + ar(n-2)+ ar(n-1) | |
| 接下来,把 S 乘以 r: | S·r = | ar + ar2 + ar3 + …… + ar(n-1) + arn |
留意到 S 和 S·r 很相似吗?
把它们相减!
哈!中间的项差不多全消去了。
(酷!)
把 S·r 从 S 减去,结果是:
S − S·r = a − arn
重排来求 S:
| 分解因数 S 和 a: | S(1−r) = a(1−rn) | |
| 除以 (1-r): | S = a(1−rn)/(1−r) |
这就是我们要导出的公式(厉害!):
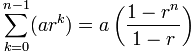
无穷等比级数
当 n 趋近无穷大时会怎么样?
……若 r 小于 1,rn 会趋近 零,结果是:
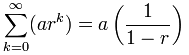
注意:若 r 是 1 或大于 1(或小于 -1),以上便不管用:
r 必须是在 -1 和 1 之间(但不包括 1 和 -1)
并且,r 也不能是 0,因为数列会变成 {a,0,0……},不是等比数列了
再看看以上的例子:
例子:把每项小一半的数列的所有的项加起来:
{ 1/2,1/4,1/8,1/16…… }
已知:
- a = 1/2(首项)
- r = 1/2(每项小一半)
所以:
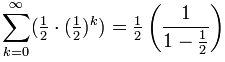
= ½ × 1 / ½ = 1
对了……(1/2)+(1/4)+(1/8)+……
还不相信?看看这正方形: 把(1/2)+(1/4)+(1/8)+……加起来 ……我们得到整个正方形! |
 |
循环小数
在另一个网页中我们问:"0.999……是不是等于 1?"我们来算算:
例子:计算 0.999……
循环小数可以写成这样:
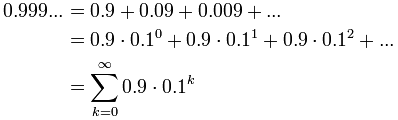
现在可以用公式:
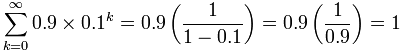
惊艳!0.999…… 真的等于 1。
……等比数列和它的和非常有用。