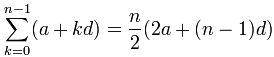等差数列及它的和

数列

序列是一组顺序排列的东西，若这些东西是数，我们便称之为数列。

等差数列

在等差数列里， 每一项和下一项的差是个常数。

换句话说，每次加个等值，至到永远，……

例子：

1，4，7，10，13，16，19，22，25……

每项和下一项的差是 3。

等差数列的一般写法是：

{a, a+d, a+2d, a+3d, ... }

a 是首项，
d 是项与项之间的差（叫"公差"）

例子：（续）

1，4，7，10，13，16，19，22，25……

有：

a = 1 （首项）
d = 3 （项与项之间的 "公差"）

数列是：

{a，a+d，a+2d，a+3d……}

{1，1+3，+2×3，1+3×3……}

{1，4，7，10……}

规则

我们可以把等差数列写成一个公式：

x_n = a + d(n-1)

（用 "n-1"，因为在第一项里没有 d）

例子：写下以下数列的规则，并求其第四项。

3，8，13，18，23，28，33，38……

每项和下一项的差是 5。

a 和 d 的值是：

a = 3 （首项）
d = 5 (（"公差"）

计算出规则：

x_n = a + d(n-1)

= 3 + 5(n-1)

= 3 + 5n - 5

= 5n - 2

所以第 4 项是：

x₄ = 5×4 - 2 = 18

自己来检验！

把等差数列加起来

把等差数列的项加起来：

a + (a+d) + (a+2d) + (a+3d) + ...

用这个公式：

总和符号

那个符号是什么？这是总和符号

意思是 "加起来"

符号的下面和上面是开始值和结束值：

总和符号

意思是："以 n 从 1 到 4，把 n 加起来。答案=10

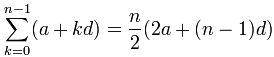
使用方法：

例子：把以下的等差数列的头 10 项加起来：

{ 1，4，7，10，13…… }

a、d 和 n 的值是：

a = 1 （首项）
d = 3 （"公差"）
n = 10 （相加多少项）

所以：

总和符号

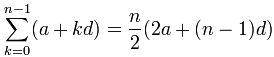
变成：

总和符号

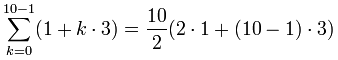
= 5(2+9·3) = 5(29) = 145

检验：你自己把项加起来看看是不是等于 145！

为什么公式是这样的？

我们来看看为什么公式是这样的，我们会用一个有趣的技巧。

首先，设"S"为数列的和：

S = a + (a + d) + ... + (a + (n-2)d) + (a + (n-1)d)

接下来，把 S 再写一遍，不过这次反过来写：

S = (a + (n-1)d) + (a + (n-2)d) + ... + (a + d) + a

逐项相加：

S	=	a	+	(a+d)	+	...	+	(a + (n-2)d)	+	(a + (n-1)d)
S	=	(a + (n-1)d)	+	(a + (n-2)d)	+	...	+	(a + d)	+	a

2S	=	(2a + (n-1)d)	+	(2a + (n-1)d)	+	...	+	(2a + (n-1)d)	+	(2a + (n-1)d)

每项都是一样的！总共有 "n" 项，所以……

2S = n × (2a + (n-1)d)

除以 2：

S = (n/2) × (2a + (n-1)d)

这就是我们要导出的公式：

总和符号