大自然、黄金比例
与斐波那契……

有些植物以螺旋形状生长，例如这些向日葵籽。

螺旋自然形成，因为每个细胞在旋转之后诞生。

"新细胞，然后旋转、
然后再生一个细胞，然后旋转……"

多少旋转？

如果你是植物，在每个细胞之间你要转多远？

如果不转，结果就是条枝干。

但是这样不行……你需要圆的形状，并且中间没有空间。

自己试试求最好的答案？

尝试用不同的数值，例如 0.75、0.9、3.1416、0.62 等等。

记住，你要的是从头到尾都没有缺口的图案：

 

（还有，整数的部分，例如 1. 或 5.对结果是没有影响的，因为整数的旋转就是转回到原来的方向。）

你得到什么结果？

如果你的答案的最后几个数位是 0.618 （或 0.382，等于 1 − 0.618），那我得说："恭喜你，植物学大师！"

这是因为黄金比例（1.61803……）是最好的答案，而向日葵自己自然地发现了这秘密！ 自己来试试……应该像这样。

为什么？

任何简单分数（例如：0.75 是 3/4、0.95 是 19/20 等等）最终都会形成像一条条枝干的图案，而且图案里会有空间。

但黄金比例（符号是希腊语字母 Phi，如左）不是分数。 它是个无理数（意思是不能写成简单分数），它也是……最不像分数的数。

黄金比例其中的一个特性是可以自我定义：
	（以数字表示就是：1.61803…… = 1 + 1/1.61803……）
这可以展开为这个无穷延续的分数（叫"连分数"）：

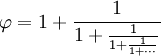所以它存在于简单分数之间。

斐波那契数

黄金比例与斐波那契数（0、1、1、2、3、5、8、13、21 ……，每项是上两项的和）有特别的关系。

两个连续斐波那契数的比很接近黄金比例：

A	B		B / A
2	3		1.5
3	5		1.666666666……
5	8		1.6
8	13		1.625
13	21		1.615384615……
……	……		……
144	233		1.618055556……
233	377		1.618025751……
……	……		……

所以，就像用 0.142857 (1/7) 会得到七条枝干的图案，用黄金比例会得到斐波那契数。

尝试数数螺旋枝干――"向左转"的螺旋枝干，向"右转"的螺旋枝干 …… 你得到什么数？

螺旋形树叶生长

不只在向日葵上，这个有趣现象在大自然里很多地方都可以看到。

树叶、树枝和花瓣也可以跟随螺旋的形状生长。

为什么？为了新树叶不挡住照着旧树叶的阳光，并且最多的雨水或露水能流到根部。

 

如果植物有螺旋形的生长，旋转的大小时常是两个连续斐波那契数的比，例如：

• 半个转是 1/2（1 和 2 是斐波那契数），
• 3/5 也常见（也是斐波那契数），
• 5/8 也是！

越来越趋近黄金比例。

这就是为什么斐波那契数时常在植物里出现。 1、2、3、5、8、13、21 …… 在大自然里无处不在。 这是有 21个花瓣的雏菊 （但可能会多几块或者少几块，因为 有些花瓣可能掉了或还在生长）

可是，不是所有的植物都是这样的，大自然里有无数的生存方法。

黄金角

我们在上面讲的是"旋转"（全转）。

0.61803…… 转等于 222.4922……度，大约 222.5°。

相反方向大约是 137.5°。称为 "黄金角"。

 

下次在花园里，留意寻找黄金角，
数花瓣和树叶来找斐波那契数，
体验大自然的智慧！

练习

你现在可以去花园数树叶和花瓣，同时测量植物的旋转来看看可以发现什么有趣的事实。

把结果填到这个表里：

植物名字或描述：
叶子螺旋形生长吗？ 是 / 否
数一组叶子：
	有几片叶子（a）？
	有几个全转（b）？
	每片叶转多少（b/a）：
	旋转角度（360 × b/a）：
有花朵吗？ 有 / 无
	花 1 有几个花瓣：
	花 2：
	花 3：

（不要忘记，大自然有自己的规律，不一定要跟随数学，
但也时常与数学有奇妙的吻合。）