组合与排列

有什么分别？

我们在使用 "组合" 这个词时，通常都不会讲究物件的次序。换句话说：

	*"我的水果沙拉是苹果、葡萄和香蕉的组合"* 我们并不理会水果的次序，我们可以说："香蕉、葡萄和苹果" 或 "葡萄、苹果和香蕉"。都是同样的水果沙拉。

	*"保险箱的密码是 472"。这个数字组合的次序就重要了。"724" 打不开保险箱。"247" 也不行。一定要是 4-7-2*。

因此，在数学中我们用精确的语言：

	如果次序不重要，就叫组合。
	如果次序重要就叫排列。

比较精确的名字应该是 "排列锁"！

换句话说：

排列是有序的组合。

记住：要 "排" 列就需要次序，不然堆成一 "组" 就可以了……

排列

有两种基本排列：

可重复：像暗码锁的暗码。暗码可以是 "333"。
不可重复：例如赛跑的首三名。一个人不能同时是第一名和第二名。

一、重复排列

这是最容易计算的。

当一个东西有 n个不同类型时 …… 我们每次就有 n 个选择！

例如：选 3个，排列是：

n × n × n
（n 自乘 3次）

一般来说：从有 n个不同类型的东西里选 r个的排列是：

n × n × ...（r次）

（换句话说，选第一个时有 n个可能，然后选第二个时也有 n个可能，依此类推，每次乘以 n。）

用 r 的指数来写比较简单：

n × n × …… （r次） = n^r

例子：暗码锁的暗码有三个数字，每个数字可以是（0、1、2、3、4、5、6、7、8、9）里的其中一个：

10 × 10 × … （3次） = 10³ = 1,000个排列

公式就是：

n^r

其中 n 是被选择的东西的个数，而我们要选 r次
（可以重复，次序重要）

二、不重复排列

在这个情况下，每选一个后我们就要把选择的可能减少一个。

例如，16个桌球有几个不同次序的排列？

选了 "14" 号球后，我们不能再选它，所以剩下来的选择可能就少了一个。

因此：第一个由 16个可能，第二个只有 15个可能，接下来就是 14，13 等等。排列的总数是：

16 × 15 × 14 × 13 × … = 20,922,789,888,000

但我们可能只需要选 3个球，所以排列个数只是：

16 × 15 × 14 = 3,360

换句话说，有 3,360 不同的方法去从 16个球里排列 3个球。

不可以重复，选择可能每次减少一个。

怎样用数学语言来描述呢？答案：用 "阶乘函数"

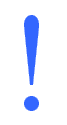阶乘函数 （符号： !）的意思是把一系列逐项减小的自然数相乘。例子：

4! = 4 × 3 × 2 × 1 = 24
7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5,040
1! = 1

注意：惯例是 0! = 1。很有趣，没有数字相乘的结果是 1！不过使用这个惯例，我们可以简化很多方程。

所以，选所有桌球的排列是：

16! = 20,922,789,888,000

但如果我们只选 3个，我们不需要乘以 14 以下的数。我们怎样表达这个呢？除以 13!

16 × 15 × 14 × 13 × 12 …		= 16 × 15 × 14 = 3,360
13 × 12 …		= 16 × 15 × 14 = 3,360

留意 16! / 13! = 16 × 15 × 14

公式是：

n!(n − r)!

其中 n 是被选择的东西的个数，而我们在其中需要选 r个
（不重复，次序重要）

例子："16个球里排列 3个"是：

16!	=	16!	=	20,922,789,888,000	= 3,360
(16-3)!		13!		6,227,020,800

（等于： 16 × 15 × 14 = 3,360）

例子：10个人里可以有几个第一和第二的排列？

10!	=	10!	=	3,628,800	= 90
(10-2)!		8!		40,320

（等于： 10 × 9 = 90）

记法

还有更简单的记法，不需要把整个公式写出来：

例子：P(10,2) = 90

组合

有两种组合（次序不重要）：

可重复：例如口袋里的硬币 (5,5,5,10,10)
不可重复：例如彩票号码 (2,14,15,27,30,33)

一、重复组合

这个最难解释，我们待会儿再讲。

二、不重复组合

这就是彩票背后的原理。数字逐个抽出来，如果抽出我们选择了的号码（不论次序），我们就中奖了！

最简单的解释是：

假设次序重要（即是排列），
然后调整为次序不重要的答案。

回到上面桌球的例子，假设我们只需要知道选了哪 3个桌球，而次序不重要。

上面计算量 16 选 3 有 3,360个不同排列。

但如果次序不重要，其中很多排列就变成相同的了！

例如，假设选了 1、2 和 3 号球。有以下可能：

次序重要	次序不重要
1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1	1 2 3

所以排列比组合有大 6倍的可能。

我们可以用上面排列的公式来计算 "1 2 3" 可以有几个不同排列。答案是：

3! = 3 × 2 × 1 = 6

（另一个例子：4样东西可以有 4! = 4 × 3 × 2 × 1 = 24 个不同排列方法。你可以自己去试试！）

因此，如果次序不重要，我们就需要把排列的公式以选择出来的东西的排列个数减小：

这个公式非常重要，它有自己的记法：

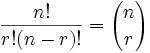其中 n 是被选择的东西的个数，我们在其中需要选 r个
（不重复，次序不重要）

通常可以这样说："n 取 r"（例如 "16 取 3"）

也称为二项系数。

记法

除了用上面的 "大括号"，也可以用以下的记法：

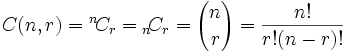
组合记法：C(n,r) = nCr = ( n r ) = n!/r!(n-r)!

要牢记这个公式：

n!r!(n − r)!

例子

桌球的例子就是（次序不重要）：

16!	=	16!	=	20,922,789,888,000	= 560
3!(16-3)!		3!×13!		6×6,227,020,800

也可以这样做：

16×15×14	=	3360	= 560
3×2×1		6

留意公式的对称:

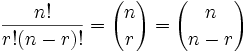
n!/r!(n-r)! = ( n r ) = ( n n-r )

换句话说，16 取 3 和 16 取 13 是相等的。想想：每一次选要的 3个时，你也选了剩下的 13个不要，所以选 3个和选 13个的组合个数是相同的。

16!	=	16!	=	16!	= 560
3!(16-3)!		13!(16-13)!		3!×13!

杨辉三角

我们也可以用杨辉三角来计算这些数值。去第 "n" 行（顶行是第 0），然后向右 "r" 个位就是合适的数值。这是第 16行附近：

1    14    91    364  …

1    15    105   455   1365  …

1    16   120   560   1820  4368 …

一、重复组合

现在我们来看重复组合 ……

冰激凌

有五种冰激凌口味：香蕉、巧克力、柠檬、草莓和香草。

我想要三球（节食？什么节食？）。有几个选择？

我们用英语字母来代表口味：{b, c, l, s, v}。这是一些选择：

{c, c, c}（3 球巧克力）
{b, l, v}（香蕉、柠檬和香草各一球）
{b, v, v}（一球香蕉，两球香草）

（就是：从 n=5个东西里选 r=3个。
次序不重要，可以重复！）

我不可以描述怎样计算答案，但我可以告诉你一个特别技巧。

bclsv

想象冰激凌在桶五个桶里。我们可以说："向右移到下一个桶，挖三球，再移过三个桶"。这样就有 3球巧克力了！

就好像命令一个机械人去挖冰激凌！

我们可以用图来显示：（箭头代表移，圆代表挖）。

上面的三个例子就是这样：

{c, c, c}（3球巧克力）：
{b, l, v}（香蕉、柠檬和香草各一球）：
{b, v, v}（香蕉一球、香草两球）：

我们现在可以不考虑口味，我们有一个更简单的问题："有几个方法排列箭头与圆？"

注意一定有 3个圆（3个球）和 4个箭头（向右移 4次）。

所以有 r + (n−1) 个位置，而我们要在 r个位置放个圆。

就像："有 r + (n−1)个桌球，我们要选 r个"。现在问题和上面的桌球例子一样，不过数字有点不同：

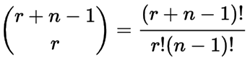其中 n 是被选择的东西的个数，我们在其中要选 r个
（可以重复，次序不重要）

如果我们选箭头，就是 "有 r + (n−1)个位置，要在 (n−1)个位置放个箭头"，答案是一样的：

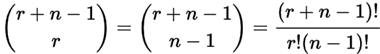
( r+n-1 r ) = ( r+n-1 n-1 ) = (r+n-1)!/r!(n-r)!

那么，这个例子的答案是多少？

(3+5−1)!	=	7!	=	5040	= 35
3!(5−1)!		3!×4!		6×24

有 35个不同的组合去在 5种口味里选 3球冰激凌。

结论

我们讲了很多。我建议你再看一遍这个页面！

但是，了解这些公式背后的原理只是个开始，在现实生活里应用这些公式也不容易。

至少你现在懂得怎样计算这 4个情况的排列与组合了："次序重要/不重要" 以及 "可/不可重复".

活动：子集