二项分布
"二项" 在这里的意思是关于有"二"个 …… |
 |
 |
|
抛硬币:
|
我们说:硬币正面向上(H)的概率是 ½ |
||
 |
掷骰子:
|
| 我们说:四 的概率是 1/6 (六面里有一面是四)。 不是四的概率是 5/6 (六面里有五面不是四) |
|
来抛硬币!
抛一个公平的硬币三次 …… 结果是两个正面的概率是多少?
抛一个公平的硬币三次(H 是正面, T 是反面)可以有 8 个结果:
| HHH |    |
|
| HHT |    |
|
| HTH |    |
|
| HTT |    |
|
| THH |    |
|
| THT |    |
|
| TTH |    |
|
| TTT |    |
我们想要的是哪些结果?
"两个正面" 可以是任何次序: "HHT"、"THH" 和 "HTH" 都有两个正面(和一个反面)。
所以 3个结果有 "两个正面"。
每个结果的概率是多少?
每个结果的可能性是一样的,一共有 8 个可能,所以每个结果的概率是 1/8
所以结果是"两个正面"这个事件的概率是:
| 需要的 结果 |
每个结果的 概率 |
||
| 3 | × | 1/8 | = 3/8 |
有特别的名词:
- 结果:抛三次硬币的结果(8 个可能)
- 事件: 三次里有"两个正面" (3个可能)
我们来计算所有的概率:
计算是这样的(P 的意思是 "概率"):
- P(三个正面) = P(HHH) = 1/8
- P(两个正面) = P(HHT) + P(HTH) + P(THH) = 1/8 + 1/8 + 1/8 = 3/8
- P(一个正面) = P(HTT) + P(THT) + P(TTH) = 1/8 + 1/8 + 1/8 = 3/8
- P(没有正面) = P(TTT) = 1/8
我们可以用 随机变量 X = "抛 3次硬币里结果是正面的次数":
- P(X = 3) = 1/8
- P(X = 2) = 3/8
- P(X = 1) = 3/8
- P(X = 0) = 1/8
我们也可以画个 柱形图:
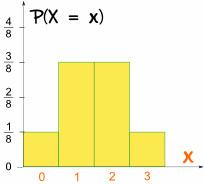
图是对称的!
做个公式
好 …… 抛 9次硬币里得到 5个正面 的可能性是多少 …… 把全部结果 (512) 写下来要花很多花时间!
我们还是做个公式吧。
在上面的例子里,我们怎样可以得到 1、3、3 和 1 这些值呢?
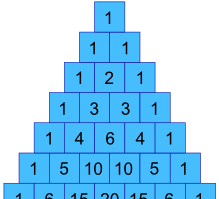 |
这些值是 杨辉三角 的第三行 …… !
我们可以用一个公式来计算这些值吗? |
可以的,像这样: |
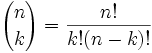 |
|
|
||
通常这个是叫 "n取k"。你可去 注意: "!" 的意思是 "阶乘",例如 4! = 1×2×3×4 = 24 |
||
学以致用:
例子:抛 3次,结果有 2个正面
n=3 和 k=2
| n! | = | 3! | = | 3×2×1 | = 3 |
| k!(n-k)! | 2!(3-2)! | 2×1 × 1 |
有 3个结果是有 "2个正面" 的
(在上面我们数出来了,不过这里是用公式算出来的。)
现在我们用这个公式来解一个比较难的问题:
例子:抛 9次,结果有 5个正面的可能性是多少?
n=9 和 k=5
| n! | = | 9! | = | 9×8×7×6×5×4×3×2×1 | = 126 |
| k!(n-k)! | 5!(9-5)! | 5×4×3×2×1 × 4×3×2×1 |
抛 9次有 29 = 512个可能结果,所以可能性是:
| 我们想要的 结果的次数 |
每个结果的 概率 |
|||
| 126 | × | 1 | = | 126 |
| 512 | 512 |
| P(X=5) = | 126 | = | 63 | = 0.24609375 |
| 512 | 256 |
差不多 25% 的可能性。
(比全部写下来容易点。)
偏差!
在上面讲的情况里,成功和失败的可能性是相同的。
可是,当硬币有偏误(不公平的硬币)时,一面的可能性便会大于另一面。
例子:你卖三明治,70% 的人买鸡肉三明治,其他的买猪肉。
接下来的三个顾客买两个鸡肉三明治的概率是多少?
这和抛硬币差不多,不过可能性是 70/30 而不是 50/50。
我们画个 树图:

图中突出显示了有 "两个鸡肉" 的结果。
注意所有 "两个鸡肉" 的概率全是 0.147,因为每次都是把两个 0.7 和一个 0.3 相乘。
我们可以用公式来求 0.147 这个值吗?公式里需要有 "两个 0.7 和一个 0.3"
- 0.7 是我们想要的结果的概率,称它为 p
- 2 是我们想要的结果的个数,称它为 k
并且
- 其他的结果的概率是:1-p
- 一共有 n 个结果
- 其他的结果的个数是:n-k
所以所有的结果一同发生的概率是:
pk(1-p)(n-k)
例子:(续)
- p = 0.7 (鸡肉的概率)
- n = 3
- k = 2
这就是:
pk(1-p)(n-k) = 0.72(1-0.7)(3-2) = 0.72(0.3)(1) = 0.7 × 0.7 × 0.3 = 0.147
这便是每个结果的概率。
结果的总数是:
| n! | = | 3! | = | 3×2×1 | = 3 |
| k!(n-k)! | 2!(3-2)! | 2×1 × 1 |
这就是:
| 我们想要的 结果 |
每个结果的 概率 |
|||
| 3 | × | 0.147 | = | 0.441 |
所以 "3个人里面有 2个人买鸡肉三明治" 这个事件的概率 = 0.441
好了,做了这么多,其实我们已经知道这个答案了,不过现在我们可以解比较复杂的问题了。
例子:"因为 70% 的人选鸡肉,所以下 10个顾客里有 7个会买鸡肉" …… 这句话是对的可能性是多少?
- p = 0.7
- n = 10
- k = 7
公式说:
pk(1-p)(n-k) = 0.77(1-0.7)(10-7) = 0.77(0.3)(3) = 0.0022235661
这是每个结果的概率。
结果的个数是:
|
最后得到:
| 我们想要的 结果 |
每个结果的 概率 |
|||
| 120 | × | 0.0022235661 | = | 0.266827932 |
实际上 10个顾客里有 7个买鸡肉三明治的可能性只是差不多 27%
这个故事的寓意是:就算长期平均是 70%,不要期望下 10个里会有 7个。
结合起来
我们知道怎样去求数量:
| n! |
| k!(n-k)! |
还有每个结果的概率:
pk(1-p)(n-k)
把它们相乘:
n个里有 k个的概率:
| P(n取k) = | n! | pk(1-p)(n-k) | |
| k!(n-k)! |
二项分布概率公式
重要提示:
- 试验是独立的,
- 每个试验只有两个可能结果,
- 每个试验里的 "成功" 概率是不变的。
梅花机
来玩玩 梅花机 (然后去阅读 梅花机解释)来更多了解二项分布。

掷骰子
掷一个公平的骰子四次。求得到以下结果的概率:
- 0 个二点
- 1 个二点
- 2 个二点
- 3 个二点
- 4 个二点
n=4, p = P(二点) = 1/6
X 是这个随机变量:"掷四次骰子里得到二点的次数"。
把 x = 0 到 4 代入到公式里:
| P(n取k) = | n! | pk(1-p)(n-k) |
| k!(n-k)! |
像这样(确到 4个小数位):
- P(X = 0) = (4!/0!4!) × (1/6)0(5/6)4 = 1 × 1 × (5/6)4 = 0.4823
- P(X = 1) = (4!/1!3!) × (1/6)1(5/6)3 = 4 × (1/6) × (5/6)3 = 0.3858
- P(X = 2) = (4!/2!2!) × (1/6)2(5/6)2 = 6 × (1/6)2 × (5/6)2 = 0.1157
- P(X = 3) = (4!/3!1!) × (1/6)3(5/6)1 = 4 × (1/6)3 × (5/6) = 0.0154
- P(X = 4) = (4!/4!0!) × (1/6)4(5/6)0 = 1 × (1/6)4 × 1 = 0.0008
总结:"掷 4次,有 48% 的机会没有二点、39% 的机会有 1个二点、12% 的机会有 2个二点、1.5% 的机会有 3个二点和小小的 0.08% 的机会全部的投掷都是二点(机会很小,但不是不可能!)"
在这个例子里,柱形图不是对称的:
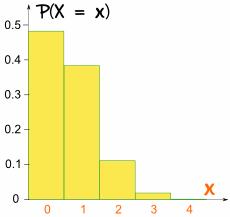
不是对称的!
图是偏斜的,因为 p 不是 0.5

运动自行车
你的公司制造运动自行车。90% 的运动自行车通过最后质量检查(10% 不通过,需要修补)。
首先求所有的概率。
- n = 4,
- p = P(通过) = 0.9
X 是代表 "在四个质量检查里通过的个数" 的随机变量
把 x = 0 到 4 代入到公式里:
| P(n取k) = | n! | pk(1-p)(n-k) |
| k!(n-k)! |
像这样:
- P(X = 0) = (4!/0!4!) × 0.900.14 = 1 × 1 × 0.0001 = 0.0001
- P(X = 1) = (4!/1!3!) × 0.910.13 = 4 × 0.9 × 0.001 = 0.0036
- P(X = 2) = (4!/2!2!) × 0.920.12 = 6 × 0.81 × 0.01 = 0.0486
- P(X = 3) = (4!/3!1!) × 0.930.11 = 4 × 0.729 × 0.1 = 0.2916
- P(X = 4) = (4!/4!0!) × 0.940.10 = 1 × 0.6561 × 1 = 0.6561
总结:"在下四个质量检查里,只有小小的 0.01% 机会没有自行车通过检查、0.36% 的机会有 1辆通过、5% 的机会有 2辆通过、29% 的机会有 3辆通过和 66% 的机会所有有都通过。"
平均、方差和标准差
这些都有相当简单的公式。证明这些公式有点复杂,但公式是管用的!
平均值,也叫 "期望值",是:
μ = np
在运动自行车质量检查的例子里:
μ = 4 × 0.9 = 3.6
我们期望每 4辆自行车里有 3.6辆通过检查。
有道理 …… 0.9 的机会乘以4辆车等于 3.6
方差的公式是:
方差:σ2 = np(1-p)
标准差是方差的平方根:
σ = √(np(1-p))
运动自行车例子:
方差:σ2 = 4 × 0.9 × 0.1 = 0.36
标准差是:
σ = √(0.36) = 0.6
注意:也可以做个列表来用人手计算:
| X | P(X) | X × P(X) | X2 × P(X) |
| 0 | 0.0001 | 0 | 0 |
| 1 | 0.0036 | 0.0036 | 0.0036 |
| 2 | 0.0486 | 0.0972 | 0.1944 |
| 3 | 0.2916 | 0.8748 | 2.6244 |
| 4 | 0.6561 | 2.6244 | 10.4976 |
| 总和: | 3.6 | 13.32 |
平均是 (X × P(X)) 的总和:
μ = 3.6
方差是 (X2 × P(X)) 的总和 减去 平均2:
方差:σ2 = 13.32 − 3.62 = 0.36
标准差是:σ = √(0.36) = 0.6
答案和上面的一样(还好!)
总结
二项分布概率公式
| P(n取k) = | n! | pk(1-p)(n-k) |
| k!(n-k)! |
X 的平均值:μ = np
X 的方差:σ2 = np(1-p)
X 的标准差:σ = √(np(1-p))
