梅花机解释
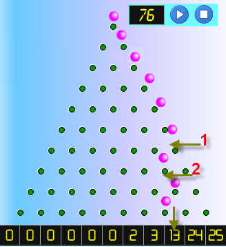
梅花机 又称为 "高尔顿板" (以弗朗西斯·高尔顿爵士命名)是一个以三角形交错排列的垂直钉子列阵(来玩玩!)
在球上端的钉子放下小球,小球落下时会碰到钉子,最终落到底端的格子里。
当小球碰到钉子后会向左或向右落下。
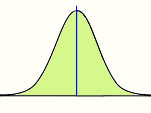
有趣的是:当碰到钉子时向左和向右落下的概率是相等时,在低端的小个子里的小球会形成典型的标准正态分布形状。
(如果概率不是相等的话,形状便会是 "偏斜" 的标准正态分布。)
公式
我们可以计算有关的概率!
这样想:如果小球有k次碰到钉子时向左落下,它便会落到离右端 k个位置的格子里。
在这例子里,小球向左落下了两次,其他的都是向右。小球最后落到离右端两个位置的格子里。
一般来说,若梅花机有 n行钉子,则小球可以在碰到钉子时向左落下 k次和向右落下 (n-k)次。
两边的概率通常都是 50%,但有时也可以是 60%-40% 等。
设向左落下的概率为 p,向右落下的概率便是 (1-p),我们便可以计算任何一条小球经过的路线的概率:
| 小球向钉子的左边落下的概率是 p,向左落下 k次的概率是:pk | ||
| 其他 (n-k)次的概率是:(1-p)(n-k) | ||
| 所以这条路线的概率是 pk(1-p)(n-k) |
但可以有很多这样的路线!例如,向左落下可以是在第一行和第二行,或第一行和第三行,或第二行和第七行等等。
我们可以把全部的路线都写下来(LLRRR……、LRLRR……、LRRL……),但有一个更容易的方法。
有几条路线
我们可以用杨辉三角。实际上,梅花机就好像一个杨辉三角,不过用钉子而不用数字。在每一个钉子的位置的数就是可以到达那钉子的路线的个数。是不是很奇妙?
我们也可以用组合学里的这个公式:
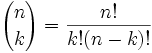
通常这是叫 "n取k",写成 C(n,k)。
它是从n物中,不计较次序取k物的不同方式的个数。
注意:"!" 的意思是 "阶乘",例如 4! = 1×2×3×4 = 24
放在一起,最后的公式是:
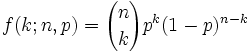
(这是 二项分布 的公式。)
例子:
10行钉子:(n=10),向左落下的概率是 0.5 (p=0.5),小球跌到从右端向左第3个格子的概率 (k=3) 是:
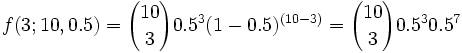
并且:
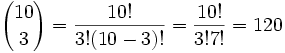
(就是说,小球可以沿 120条不同的路线
落到从右端的第3个格子里。)
所以:
![]()
我们可以为 行数=10,概率=0.5 做一个列表:
| 从右端的格子: | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 概率: | 0.001 | 0.010 | 0.044 | 0.117 | 0.205 | 0.246 | 0.205 | 0.117 | 0.044 | 0.010 | 0.001 |
| 例子:100个小球 | 0 | 1 | 4 | 12 | 21 | 24 | 21 | 12 | 4 | 1 | 0 |
当然,这是随机的,所以如果你真的去做,结果可能会和这个理论结果不相同。
又一个例子:
概率是 0.8,列表便是这样:
| 从右端的格子 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 概率 | 0.107 | 0.268 | 0.302 | 0.201 | 0.088 | 0.026 | 0.006 | 0.001 | 0.000 | 0.000 | 0.000 |
| 例子:100 个小球 | 11 | 26 | 30 | 20 | 9 | 3 | 1 | 0 | 0 | 0 | 0 |
自己来试试
放 100(或更多)个小球进梅花机来看看得到什么结果。研发这个软体时我做过很多次,但我从来没有得到过理论结果,不过通常都是非常接近理论结果的。祝你好运!