正态分布
数据可以用不同的方式"分布" (散布)。
| 数据可以 向左散布的多一些 |
或向右散布的多一些 |
|
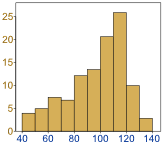 |
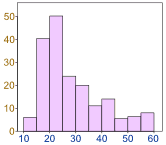 |
|
| 或乱七八糟的 |
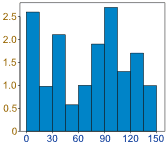 |
但数据经常会集中在一个中心值的附近,而不向左或右偏斜,像一个 "正态分布":
正态分布
"钟形曲线"是个正态分布。
黄色的直方图显示有些数据遵循,
但并不完美地遵循,正态分布(通常是这样的)。
 |
通常这就叫做 "钟形曲线" 因为曲线的形状像个钟。 |
实际生活中很多东西都遵循正态分布:
- 人的身高
- 机器产品的大小
- 测量误差
- 血压
- 测验分数
我们说数据是 "正态分布"的:
正态分布:
梅花机
你可以来看看随机形成的正态分布! 这叫梅花机――一个很奇妙的机器。 来玩玩! |
 |
标准差
标准差是数据散布的指标(去网页看看它是怎样计算的)。
当你计算标准差时,你通常会留意到:
68%的数值是在
95%的数值是在 2个标准差之内
99.7%的数值是在 |
例子:学校里 95%的学生的身高是在 1.1m 与 1.7m之间。
假设数据是正态分布的,求平均值和标准差。
平均是在 1.1m 和 1.7m 的正中间:
平均 = (1.1m + 1.7m) / 2 = 1.4m
95% 是平均两边 2个标准差的距离(总共 4个标准差),所以:
| 1个标准差 | = (1.7m − 1.1m) / 4 |
| = 0.6m / 4 | |
| = 0.15m |
结果是:
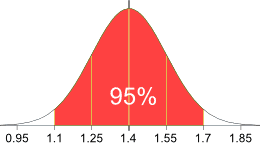
知道标准差是很有用的,因为我们可以说任何一个数值离平均值值:
- 很可能在 1个标准差之内(100个里应该有 68个是这样)
- 极有可能在 2个标准差之内(100个里应该有 95个是这样)
- 差不多必然在 3个标准差之内(100个里应该有 99.7个是这样)
标准差比值
数值离开平均值的距离与标准差的比(就是离开平均值有几个标准差)也叫 "标准分数",英语 "sigma" 或 "Z分数"。记住这些名词!
例子:在学校里有一个学生的身高是 1.85m
从图上的钟形线你可以看到 1.85m是离平均值(1.4) 3个标准差,所以: 他身高的 "Z分数" 是 3.0 |
 |
我们也可以计算 1.85 离平均值有多少个标准差
1.85 离平均值有多远?
离平均值 1.85 - 1.4 = 0.45m
这是几个标准差?标准差是 0.15m,所以:
0.45m / 0.15m = 3个标准差
所以要将数值转换为标准分数("Z分数")::
- 先减去平均值,
- 再除以标准差
这个运算叫 "标准化":
我们可以将任何正太分布转换为标准正态分布。
例子:行程时间
每天行程时间调查的结果是(分钟):
26、33、65、28、34、55、25、44、50、36、26、37、43、62、35、38、45、32、28、34
平均是 38.8分钟,标准差是 11.4分钟(你可以 复制并粘贴到标准差计算器来看看)。
转换为 Z分数("标准分数")。
转换 26:
所以 26 离平均值 -1.12个标准差
以下是头三个的转换结果
| 原数值 | 计算 | 标准分数 (Z分数) |
| 26 | (26-38.8) / 11.4 = | -1.12 |
| 33 | (33-38.8) / 11.4 = | -0.51 |
| 65 | (65-38.8) / 11.4 = | +2.30 |
| ... | ... | ... |
在图上:
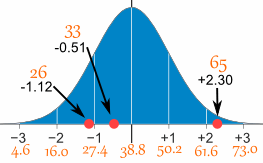
你可以自己去算其他的 Z分数!
这是我们用的 Z分数公式:
|
为什么要标准化……?
因为标准化后我们可以为数据做决定。
例子:韦教授在改卷。
这是学生的分数(满分是 60分):
20、15、26、32、18、28、35、14、26、22、17
大部分的学生连 30分也拿不到,大部分都不及格。
一定是个很难的测验,所以韦教授决定标准化所有分数,然后把合格分数定在平均以下一个标准差。
平均是 23,标准差是 6.6,以下是标准分数:
-0.45、-1.21、0.45、1.36、-0.76、0.76、1.82、-1.36、0.45、-0.15、-0.91
只有两个学生不合格(分数是 15 和 14)
标准化后的计算也比较简单,因为只需要查看一个表(标准正态分布表)而不需要每次为不同的平均值和标准差做计算。
具体来讲
以下是标准正态分布里每一半的百分比和累积百分比:
例子:你最近测验的分数是在平均值以上 0.5个标准差,有几个人的得分比你低?
- 0 与 0.5 之间是 19.1%
- 小于 0 是 50%(曲线的左半)
所以分数比你低i的百分比是:
50% + 19.1% = 69.1%
理论上 69.1% 的分数比你低(实际上百分比可能不同)

实例:你的公司包装每袋 1kg 的砂糖。
样本称量的结果是:
- 1007g、1032g、1002g、983g、1004g……(总共 100个样品)
- 平均值 = 1010g
- 标准差 = 20g
有些袋子比 1000g 轻……你可以解决问题吗?
测量的正态分布像这样:
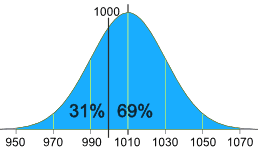
31% 的袋子比 1000g 轻,
这是欺骗顾客!
这是随机发生的,所以我们不能绝对没有比 1000g 轻的袋子,但我们可以尝试把轻的个数尽量减少。
我们把包装机器调校到 1000g 为:
- −3个标准差:
- −2.5个标准差:
我们去把机器调校到 1000g 离平均值 −2.5个标准差。
我们可以把机器调校到:
- 每袋多加一些砂糖(改变平均值),或
- 更加精确(减小标准差)
我们两个都做
调整每袋的砂糖
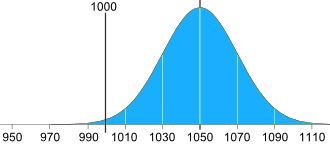
标准差是 20g,我们需要 2.5个:
2.5 × 20g = 50g
所以机器的平均值应该是 1050g,像这样:
调校机器的精确度
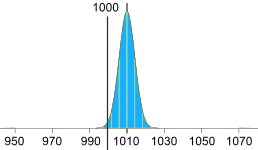
我们也可以保持平均不变(1010g),但需要 2.5个标准差等于 10g:
10g / 2.5 = 4g
所以标准差应该是 4g:
(希望机器可以这么精确!)
我们也可以两个都用:用好一点精确度和大一点重量的结合。你自己决定!
更精确的数值……
你可以用 标准正态分布表 来得到更精确的数值。