概率:独立事件

我们在生活中时常都会遇到随机事件。
你需要对这些事件有个"感觉",才能成为一个聪明和成功的人。
抛硬币、掷骰子和彩票抽奖都是随机事件的例子。
有时一个事件会影响下一个事件。
例子:从布袋里拿玻璃球:每拿走一颗玻璃球,袋子里就少一颗玻璃球,所以概率也随着改变。
这种事件叫相关事件,因为事件是与已经发生的事件有关联的(去阅读 条件概率来了解更多)。
其他不是相关的事件就是独立事件……
独立事件
独立事件是不受过去事件影响的。 这是个很重要的概念! 硬币不"知道"它以前曾经正面向上。 每一次抛掷硬币都是个绝对独立的事件。 |
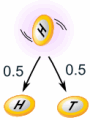 |
例子:你抛一个硬币三次,结果全是"正面"……下一次抛掷的结果也是"正面"的可能性是多少?
可能性是 ½(0.5),和任何一次抛掷一样。
以前的抛掷不会影响这次抛掷!
有些人可能想: "已经三次正面了,这一次应该轮到反面了吧",但无论如可,下一次抛掷与以前的抛掷是完全独立的。
说:"应该轮到反面了",或:"再来一次,幸运女神这次会眷顾我了" 这种行为有个名字:赌徒谬误
当然,你可能会转运,因为每个抛掷结果的概率是相同的。
独立事件的概率
"概率"(或叫"可能性")是事件发生的可能性。
我们怎样计算概率?
事件发生的概率 = 事件可能发生方式的个数 结果的总数

例子:抛一个硬币得到"正面向上"的概率是多少?
事件可能发生方式的个数:1 (正面)
结果的总数:2 (正面和反面)
所以概率 = 1 2 = 0.5

例子:掷骰子得到 "4" 点或 "6" 点的概率是多少?
事件可能发生方式的个数:2("4" 和 "6")
结果的总数:6("1"、"2"、"3"、"4"、"5" 和 "6")
所以概率 = 2 6 = 1 3 = 0.333……
表达概率的方式
概率的值可以从 0 (不可能)到 1(必然):
概率经常写成小数 或 分数。
例子:抛硬币得到"正面向上"的概率:
- 小数:0.5
- 分数:1/2
- 百分比:50%
- 或这样:二分之一
两个或多个事件
两个或多个独立事件的概率是每个事件的概率的积。
例子:连续抛到3个正面向上
每次抛掷得到 "正面" 的概率是 0.5:
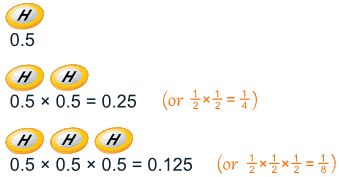
所以连续得到 3个正面向上的概率是 0.125
每次抛掷得到正面的概率是 ½,但连续得到很多个正面是不太可能的。
例子:为什么连续得到例如7个正面是不太可能,但每次抛掷有 ½ 的可能性是正面?
因为这其实是两个不同的问题:
问题 1:连续得到7个正面的概率是多少?
问题 2:在已经连续得到6个正面的条件下,下一次抛掷的结果也是正面的概率是多少?
你可以去玩玩 五点梅花器 来体验很多独立事件也可以有规律的效果。
记法
我们用 "P" 来代表 "的概率",
所以,为独立事件:
P(A 与 B) = P(A) × P(B)
A 与 B 的概率等于 A 的概率乘以 B 的概率
例子:你的老板(为公平起见)随机地选员工周末从下午4点到午夜加班2小时。
你被选中在星期六6点到8点加班的可能性是多少?
日:周末有两日,所以 P(星期六) = 0.5
时间:6点到 8点是 8小时(4点到午夜)里的 2小时 :
P(你的时间) = 2/8 = 0.25
相乘
| P(星期六 与 你的时间) | = P(星期六) × P(你的时间) |
| = 0.5 × 0.25 | |
| = 0.125 |
12.5% 的可能性
(注意:我们也可以说你想要 16个小时里的 2个小时,概率便是 2/16 = 0.125。两个方法都是正确的。)
又一个例子
想像有两组人:
- 在每组里选一个人去参加抽奖,
- 然后在这两个代表里选一个大奖中奖者:
你中大奖的可能性是多少?
- 有 1/5 的可能性 去参加抽奖
- 有1/2 的可能性 赢大奖
所以你有 1/5 的可能性,之后再有 1/2 的可能性……一起就是 1/10 的可能性:
15 × 12 = 15 × 2 = 110
我们以可以用小数来算(1/5 是 0.2,1/2 是 0.5):
0.2 x 0.5 = 0.1
你赢大奖的可能性是 0.1(1/10)。
巧合!
很多 "巧合" 其实是很可能的。
例子:房间里有30个人,你发觉小庄和莎莎的生日是相同的。
你会说:
- "真奇怪!",还是
- "这么多人,没什么稀奇的"
其实有 70% 的可能性 房间里有两个人的生日是相同的……所以事件是很可能的。
为什么概率这么高? 因为你是把每一个人与其他所有人比较(而不只是一个人与其他人比较)。 有 30人,这就是 435个比较 |
(去阅读 同一个生日 网页来了解更多。)
例子:Snap!扑克游戏
你曾经在同一时间和另一个人说同一句话吗?
真奇怪!
但你们很可能是在谈同一个话题(电影、旅游……),所以你们心中想的都很可能是一样的。
同时也不会有很多不同的句子去描述同一样东西……
……就像 "Snap!" 这个扑克游戏……
……如果你们一起说很多话,最终一定会同时说相同的话。
所以其实没甚么好大惊小怪的,不过是可能性而已。
你还可不可以想到有什么乍看是"巧合",但其实是很可能的事?
结论
- 概率是:(事件可能发生方式的个数)/(结果的总数)
- 相关事件(例如在布袋里拿玻璃球)是受过去事件影响的
- 独立事件(例如抛硬币)是不受过去事件影响的
- 2个或多个独立事件的概率是每个事件的概率的积
- 不是所有巧合都真是不太可能的(经过分析后)。