二项式定理
若你把一个二项式乘以自己……很多次,你会得到什么?
答案:
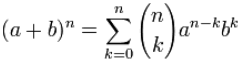
别着急……下面我会解释!
并且你会学到很多很酷的数学符号。
二项式
二项式是有二项的多项式
| 二项式例子 |
乘
二项式定理告诉我们把一个二项式乘以自己(次数不限)会得到什么。
二项式定理是基于一个规律……我们现在去发现它。
指数
首先你要了解指数是什么。 指数是指有多少个自己相乘。 |
例子:82 = 8 × 8 = 64
指数是1代表只有一个项,所以就是原来的值:
例子:81 = 8
指数是0代表一个项都没有,所以答案是 1:
例子:80 = 1
(a+b) 的指数
现在我们来看二项式。
我们用这个简单的二项式:a+b,但其实用任何二项式都可以。
从指数为0的情形开始。
指数为 0
当指数为 0,答案是 1:
(a+b)0 = 1
指数为 1
当指数为 1,答案是原项不变:
(a+b)1 = a+b
指数为 2
指数为 2 的意思是把两个自己相乘(看怎样乘多项式):
(a+b)2 = (a+b)(a+b) = a2 + 2ab + b2
指数为 3
当指数为 3,我们再乘一次:
(a+b)3 = (a+b)(a2 + 2ab + b2) = a3 + 3a2b + 3ab2 + b3
我们现在可以讲这里的规律了。
规律
上面最后的结果是:
a3 + 3a2b + 3ab2 + b3
你可以看到 a 的指数是从 3 开始,然后向下走: 3、2、1、0:
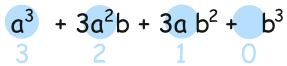
b 的指数就向上走: 0、1、2、3:
若我们把项标志为 0 到 n,便会是这样:
| k=0 | k=1 | k=2 | k=3 |
| a3 | a2 | a | 1 |
| 1 | b | b2 | b3 |
这可以写成:
an-kbk
看一个例子:
例子: 指数 n 为 3。
项是:
| k=0: | k=1: | k=2: | k=3: |
|---|---|---|---|
| an-kbk = a3-0b0 = a3 |
an-kbk = a3-1b1 = a2b |
an-kbk = a3-2b2 = ab2 |
an-kbk = a3-3b3 = b3 |
惊艳!
系数
| 现在我们已得到了: | a3 + a2b + ab2 + b3 |
| 但真正需要的是: | a3 + 3a2b + 3ab2 + b3 |
我们还没有项前面的那些数(叫系数)。
我们再来看看上面所有的结果,从(a+b)0到 (a+b)3:
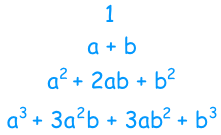
现在只看系数(如果系数没写出来,系数便是 "1"):
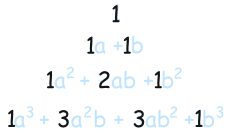
系数形成一个杨辉三角! 每个数是它上面的两个数的和(边缘除外,边缘上全是 "1")(在这里我标出了 1+3 = 4) |
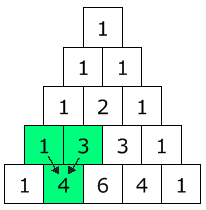 |
我们现在勇敢地试试以 4 为指数:
| a 的指数是 4、3、2、1、0: | a4 | + | a3 | + | a2 | + | a | + | 1 | ||
| b 的指数是 0、1、2、3、4: | a4 | + | a3b | + | a2b2 | + | ab3 | + | b4 | ||
| 系数 是 1、、4、6、4、1: | a4 | + | 4a3b | + | 6a2b2 | + | 4ab3 | + | b4 |
这是正确的答案。
大功告成!
我们可以用和规律来展开指数为 5、6、7、……50、……112……的二项式,任何指数!
这规律是二项式定理的精髓。
现在你可以打个盹。
醒来后自己来试试展开 (a+b)5。
答案 (悬停鼠标):a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
公式
最后我们把这规律写成一个公式。
可是, "在杨辉三角里找系数" 怎样写成公式……?
其实是有这个方程的:
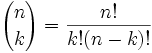 |
通常这叫 "n选取k",因为它是在n个里选取k个的不同方式的数目。 你可以在 组合和排列里了解更多 "!" 代表 "阶乘",例如 4! = 4×3×2×1 = 24 |
和杨辉三角相对是这样: (注意:最上一行是零行, |
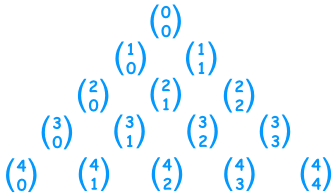 |
例子:杨辉三角里第4行,第2项是 "6".
我们来看看这公式对不对:
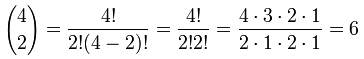
是对的!你自己去用另一个值来试试。
全部放在一起
最后我们把全部放在一起成为一个公式。
可是这里有很多东西……真的可以用一个公式写下来吗?
当然可以!我们可以用总和符号来显示不限数量的项的和:
总和符号
现在用一个公式写下来:
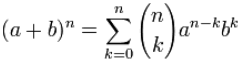
二项式定理
应用
来看看例子。
我们用来做 n = 3:
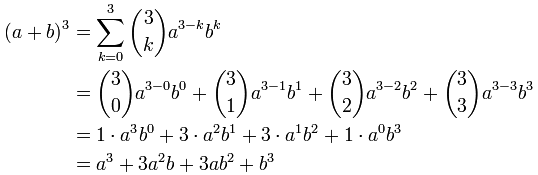
其实……通常只要记着规律就会很容易:
- 第一项的指数从 n 开始,然后向下走
- 第二项的指数从 0 开始,然后向上走
- 从杨辉三角里找系数,或用 n!/(k!(n-k)!) 来计算
像这样:
例子:(x+5)4是什么?
| 从指数开始: | x450 | x351 | x252 | x153 | x054 |
| 加上系数: | 1x450 | 4x351 | 6x252 | 4x153 | 1x054 |
然后写下答案(包括所有计算,例如 4×5, 6×52等):
(x+5)4 = x4 + 20x3 + 150x2 + 500x + 625
有时你只需要其中一项:
例子:在 (2x+4)8里,x3的系数是什么?
x3的指数是:
(2x)345
系数是 "8选取5"。我们用杨辉三角或直接计算:
n!k!(n-k)! = 8!5!(8-5)! = 8!5!3! = 8×7×63×2×1 = 56
我们得到:
56(2x)345
简化为:
458752 x3
很大的系数,对不?
最后给你一个惊艳的例子:
例子: e(欧拉数)
你可以用二项式定理去计算 e (欧拉数)。
e = 2.718281828459045……. (数字无限延续,并不重复)
它可以用以下的公式来计算:
(1 + 1/n)n
(n 越大,值越准)
这公式是个二项式,对不?我们来用二项式定理:
![(1 + 1/n)^n = 总和 k=0 to n [ (n选取k) 以 1^(n-k) 以 (1/n)^k ]](images/binomial-theorem-e.gif)
首先,我们可以拿走 1n-k,因为他永远等于 1:
![总和 k=0 to n [ (n选取k) 以y (1/n)^k ]](images/binomial-theorem-e2.gif)
同时,奇妙的是,当n趋近无穷大,大部分剩下来的都趋近 1:
剩下来的是:
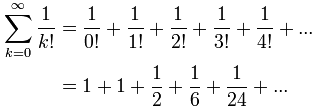
只把首几项加起来,我们得到 e ≈ 2.7083...
试试多算几项来得到更准确的近似值!
艾萨克·牛顿Isaac Newton
附注:在大约公元1665年,艾萨克·牛顿爵士发表了一个"广义"的二项式定理,它并不局限于整数的指数:0、1、2……希望将来我可以为你解释。