函数是什么?
函数显示输入与输出的关系。
 |
就好像有输入和输出的机器。 输出和输入是有关联的。 |
| f(x) | "f(x) = ... " 是一贯的标准函数记法。 |
输入、关系、输出
有很多方法去描述函数,但所有方法都有这三个主要部分:
- 输入
- 关系
- 输出
例子:"乘以 2" 是个非常简单的函数。
三个部分是:
| 输入 | 关系 | 输出 |
|---|---|---|
| 0 | × 2 | 0 |
| 1 | × 2 | 2 |
| 7 | × 2 | 14 |
| 10 | × 2 | 20 |
| …… | …… | …… |
如果输入是 50,输出是多少?
函数例子
这里我们不谈个别函数 ……
…… 我们来看函数的一般概念。
名字
首先,函数要有个名字。
最常见的名称是 "f",但也可以用其他名字,例如 "g" …… 或甚至 "果酱"。
这里我们用 "f":
我们说 "f x 等于 x 平方"
我们把函数的输入值放在函数名字后面的括号()中间:
所以 f(x) 的意思是函数叫 "f",而 "x" 是输入值
函数对输入值进行的运作:
f(x) = x2 显示函数 "f" 取输入值 "x" 的平方。
例子:f(x) = x2:
- 输入是 4
- 输出就是 16.
我们这样写: f(4) = 16。
"x" 只是个位置标志符!
"x" 只不过显示表输入值。
其实用什么符号来代表都可以!
所以这个函数:
f(x) = 1 - x + x2
和这些函数是一样的:
- f(q) = 1 - q + q2
- h(A) = 1 - A + A2
- w(θ) = 1 - θ + θ2
自变量(x、q、A等)只不过显示我们需要把输入值放在哪里:
f(2) = 1 - 2 + 22 = 3
函数有时没有名字
有时候函数没有名字,例如:
y = x2
但仍然有:
- 输入(x)
- 关系(取平方)
- 输出(y)
关系
上面我们说函数像个机器。但函数没有齿轮或传动带,也不会破坏输入!
函数显示输入与输出的关系。
"f(4) = 16" 就是说 4 和 16 是有关系的:4 → 16,而这个关系就是 f。

例子:这棵树每年长高 20厘米,所以树的高度与它年龄的关系可以用函数 h 来显示:
h(年龄) = 年龄 × 20
所以,如果年龄是 10年,高度就是:
h(10) = 10 × 20 = 200厘米
以下是这个函数的一些数值:
| 年龄 | h(年龄) = age × 20 |
|---|---|
| 0 | 0 |
| 1 | 20 |
| 3.2 | 64 |
| 15 | 300 |
| …… | …… |
函数处理什么?
最常见的是 "数字",但是 ……
|
…… 什么数字? 例如,在树的高度函数 h(年龄) = 年龄×20 里,负值的年龄是毫无意义的。 |
|
| …… 函数的输入也可以是字母("A"→"B"),或身份代码("A6309"→"及格"),或其他特别的东西。 | |
所以我们要用一个比较强大的综合工具来显示函数,这就是集合:
|
这是一些例子: 偶数集:{..., -4, -2, 0, 2, 4, ...} |
集里面的每个东西(例如 "4" 或 "帽子")叫成员或元素。
所以,函数输入一个集的元素来输出另一个集的元素。
函数是特别的
函数有特别的规则:
- 一定要可以使用于所有可能的输入
- 每一个输入值只有一个关系
这些规则可以用一个定义来表达:
函数的正式定义函数把一个集里的每一个元素 |
两个重点!
一、 |
"…… 每一个元素 ……" 的意思是 X 里的所有元素都与 Y 里的某一个元素有关系。 我们说函数覆盖 X (关系囊括所有元素)。 (但 Y 里的一些元素可能没有和 X 的元素有关系,这是允许的。) |
二、 |
"…… 独一的值 ……" 的意思是函数是单值的。一个输入值不能有多于一个输出值。 所以 "f(2) = 7 或 9" 是不行的! |
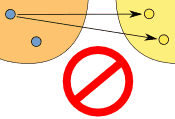
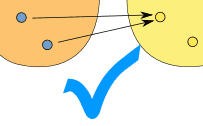
注意:"一对多关系" 是不允许的, "多对一关系" 就可以: |
||
 |
 |
|
| (一对多) | (多对一) | |
| 不允许 | 允许 | |
如果一个关系不符合这两个规则,它就不是函数 …… 它还是个关系,但不是个函数。
例子:x → x2
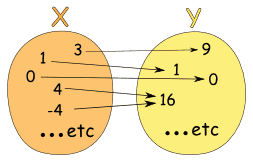
可以写成列表:
| X: x | Y: x2 |
|---|---|
| 3 | 9 |
| 1 | 1 |
| 0 | 0 |
| 4 | 16 |
| -4 | 16 |
| …… | …… |
这是个函数,因为:
- X 的每个元素都和 Y 有关系联
- X 没有元素有多于一个关系
所以这个关系符合函数的两个规则。
(注意 4 和 -4 都和 16 有关系,这是允许的。)
例子:这个关系不是函数:
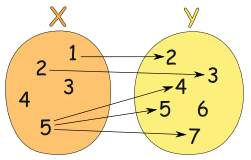
它是个关系,但不是个函数。原因是:
- X 里的 "3" 和 Y 没有关系
- X 里的 "4" 和 Y 没有关系
- X 里的 "5" 和 Y 里多于一个值有关系
(但 Y 里的 "6" 没有关系是允许的)
垂直线测试
在图上,单值的意思就是没有垂直线有多于一个交叉点。
如果有多于一个交叉点,图还是曲线,但不是函数。
有些函数有更严格的规则,去单射、满射与双射了解更多
无穷多
上面的例子只有几个数值,但函数通常是建立在有无穷多元素的集合上的。
例子:y = x3
- 输入集 "X" 是所有 实数
- 输出集 "Y" 也是所有实数
我们不能显示所有的值,所以以下只是一些例子:
| X: x | Y: x3 |
|---|---|
| -2 | -8 |
| -0.1 | -0.001 |
| 0 | 0 |
| 1.1 | 1.331 |
| 3 | 27 |
| 依此类推…… | 依此类推…… |
定义域、陪域与值域
在上面的例子里
- "X" 集的名称是定义域,
- "Y" 集的名称是 陪域,
- Y 集里与 X 有关系的元素(函数的实际输出值)的名称是值域。
你可以去阅读关于定义域、陪域与值域的特定页面来了解更多。
很多名称!
函数在数学里已经有很长的历史,也有很多不同的名称和表达方法。
以下是一些你应该知道的名词:
例子:z = 2u3:
- "u" 可以被称为 "自变量"
- "z" 可以被称为 "因变量"(它因着自变量改变)
例子:f(4) = 16:
- 我们可以叫 "4" 为 "参数"
- 我们可以叫 "16" 为 "函数的值"
序偶
这是对函数的另一个看法:
把函数的输入和输出为一个 "序偶",例如 (4,16)。
叫序偶,因为输入一定在前面,输出在后面:
(输入,输出)
像这样:
(x,f(x))
例子:
(4,16) 的意思是函数的输入是 "4",输出是 "16"
序偶集
因此,函数可以被定义为序偶的集 :
例子:{(2,4), (3,5), (7,3)} 是个这样的函数:
"2 和 4有关系"、"3 和 5 有关系"、"7 和 3 有关系"。
也注意:
- 定义域是 {2,3,7} (输入值)
- 值域是 {4,5,3} (输出值)
但函数一定要是单值的,所以我们也要说
"若集里有 (a, b) 和 (a, c),则 b 等于 c"
也即是说 "a" 值的输入不能有多于一个结果。
例子:{(2,4), (2,5), (7,3)} 不是函数,因为 {2,4} 和 {2,5} 代表 2 与 4 和 5 都有关系。
就是说,它不是函数,因为它不是单值的
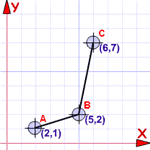 |
序偶的好处我们可以把序偶画成图 …… …… 因为序偶也是坐标! 所以坐标的集也是函数 |
函数可以有不同的部分
不同的函数输入值可以有完全不同的关系
例子:有两个部分的函数:
- 若 x 小于 0,函数的值是 5,
- 若 x 等于或大于 0,函数的值是 x2
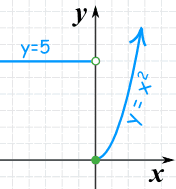 |
以下使一些数值例子:
|
去分段函数了解更多。
显与隐
最后课题:"显" 与 "隐"。
"显"函数是可以用 y=f(x) 来表示的函数,例如:
y = x3 - 3
如果知道 x 就可以求 y
这是标准的 y = f(x) 格式。
"隐"函数是不用这个格式显示的函数,例如:
x2 - 3xy + y3 = 0
已知 x,怎样求 y?
可能很困难(甚至不可能!)从 x 求 y。
"隐" 的意思是关系是 "隐"蔽的。
画图
结论
- 函数显示输入与输出的关系
- 函数把一个集(定义域的元素联系到另一个集(陪域)的元素。
- 所有的输出值(陪域里实际与定义域有关系的元素)的集叫值域
- 包含定义域里每个元素,
- 任何输入值只有一个输出值(不能是一个或另一个输出值)
- 一个输入值和它的输出值一起就叫做序偶
- 所以函数也可以被视为一个序偶的集