笛卡尔坐标
笛卡尔坐标可以在图表或地图上精确地标记你的位置。
笛卡尔坐标
笛卡尔坐标用一点 向右和向上有多远来标记它的位置:
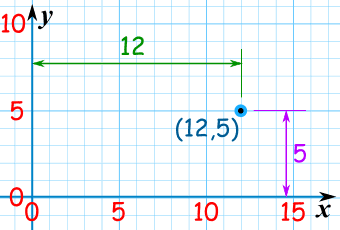 |
| 点 (12,5) 是向右 12单位,向上 5单位。 |
X轴 和 Y轴
 |
左-右(水平)的方向通常是叫 X。 |
| 上-下(垂直)的方向通常是叫 Y。 |
|
把它们一同画在图上 …… …… 就可以用笛卡尔坐标了 |
x轴和 y轴的交叉点叫 "0" 点(或 原点),
|
|
轴:测量距离的参考线.
例子:
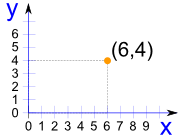
点 (6,4) 是
向右 6单位(沿 x 方向),
向上 4单位(沿 y 方向)
故此,(6,4) 的意思是:
向右走 6,向上走 4,然后 "画点"。
来玩玩!
现在最好去玩玩
来体验一下笛卡尔坐标。
像两条实数直线放在一起
就好像把两条 实数直线 放在一起,一条从左到右、一条从上到下。
方向
x 越大,位置越向右移。 |
|
y 越大,位置越向上移。 |
坐标记法
写坐标有既定的次序:
- 先写水平距离,
- 再写垂直距离。
这是叫 "序偶(也称为有序偶)" (一对有次序的数)
通常在两个数之间放个逗号,再用括号围住:
(3,2)
例子:(3,2) 代表向右 3单位,向上 2单位
例子:(0,5) 代表向右 0单位,向上 5单位。
换句话说,只是向上 5单位。
原点
点 (0,0) 有个特定名字,叫 "原点",有时用字母 "O" 来代表。
横坐标与纵坐标
你有时会看到 "横坐标" 和 "纵坐标" …… 它们只不过是 x 和 y 值:
- 横坐标:坐标里的水平("x")值:点向右多远
- 纵坐标:坐标里的垂直("y")值:点向上多远
"笛卡尔" …… ?
这坐标叫笛卡尔,因为这概念是由法国数学家和哲学家勒内·笛卡尔创立的。
这个千古名句也是他说的: "我思故我在"。
如果 X 和 Y 的值是负数呢?
和实数直线一样,坐标也可以有负值。
负:从零开始向反方向走:
- 负值的 x 向左走
- 负值的 y 向下走
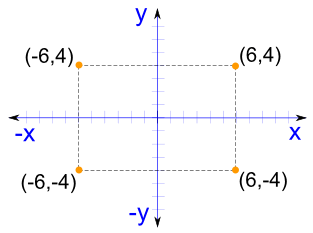 |
所以,如果是负数:
|
四象限包括负值在内,x轴和 y轴把平面空间分成四个部分: 象限 I、II、III 和 IV (数字以 逆时针 方向排列) |
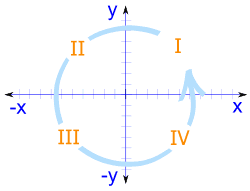 |
在象限 I,x 和 y 两者都是正数,,但 ……
- 在象限 II,x 是 负数 (y 还是正数),
- 在象限 III,x 和 y 两者都是 负数,
- 在象限 IV, x 是正数,y 是 负数。
像这样:
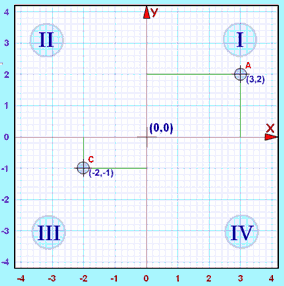 |
|
例子:点 "A" (3,2) 是向右 3单位,向上 2 单位。
x 和 y 都是正数,所以点是在象限 I"
例子:点 "C" (-2,-1) 是向右 −2单位(等于向左 2单位),向上 −1单位(等于向下 1单位)。
x 和 y 两者都是负数,所以点是在 "象限 III"
维数:1、2、3 和更多 ……
这值得思考:
| 1 | 实数直线 的方向只能是:
所以任何位置只需要一个数值来标记 |
|---|---|
| 2 | 笛卡尔坐标的方向是:
所以任何位置需要两个数值来标记 |
| 3 |
在现实世界上,我们怎样标记空间中的一点(例如你鼻尖的位置)?我们需要知道:
这是三个数值,就是 3维! |
3维
笛卡尔坐标也可以应用在 3维空间上:
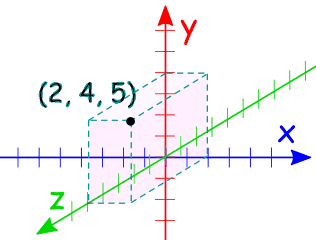 |
|
在这里,点 (2, 4, 5) 是以 三维笛卡尔坐标标记的。 |
实际上,这概念可以引申到四维或更高的空间上,但我不知道怎样画个图来给你看!