极坐标与笛卡尔坐标
。。。。。。及其互相转换。
赶时间?去看 摘要。但请先学习为什么:
有两个主要系统用来在地图或图表中准确定位:
笛卡尔坐标系
在笛卡尔坐标系中,一点是用向右和向上的距离来定位的:
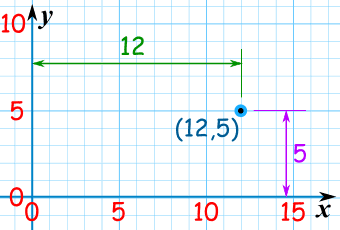
极坐标系
在极坐标系中,一点是用离中点的距离和角度来定位的:
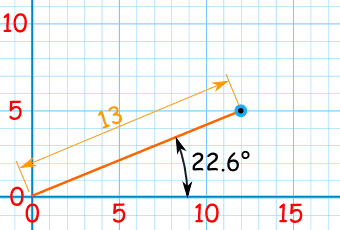
转换
从一个系统转换到另一系统,我们用这个三角形:
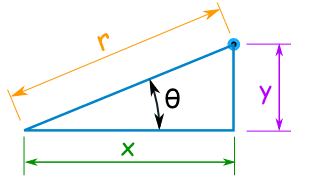
笛卡尔坐标转换为极坐标
当我们知道一点的笛卡尔坐标(x,y)想转换成极坐标(r,θ),我们需要解一个有两条已知边的直角三角形。
例子: (12,5) 的极坐标是什么?
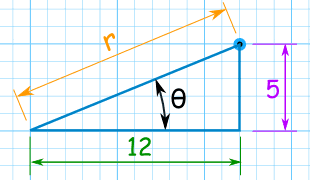
用勾股定理去计算长的一边(斜边):
用正切函数去计算角度:
答案:(12,5) 的极坐标是 (13, 22.6°)。
所以,笛卡尔坐标 (x,y) 转换为极坐标 (r,θ):
- r = √ ( x2 + y2 )
- θ = tan-1 ( y / x )
注意:当 x 或 y 是负数时,计算器可能得到错误的 tan-1 () 的值……继续看下去。
极坐标转换为笛卡尔坐标
当我们知道一点的极坐标(r, θ),想转换为笛卡尔坐标(x,y),我们需要解一个有已知斜边和角度的直角三角形:
例子:(13, 22.6°)的笛卡尔坐标是什么?
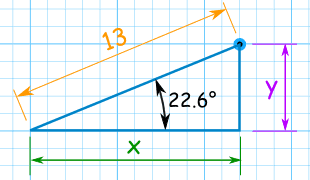
| 用 x 的 余弦函数: | cos( 22.6 °) = x / 13 | |
| 重排及解: | x = 13 × cos( 22.6 °) | |
| x = 13 × 0.923 | ||
| x = 12.002... | ||
| 用 y 的 正弦函数: | sin( 22.6 °) = y / 13 | |
| 重排及解: | y = 13 × sin( 22.6 °) | |
| y = 13 × 0.391 | ||
| y = 4.996…… |
答案: (13, 22.6°) 的笛卡尔坐标是差不多 (12, 5)。
所以,极坐标 (r,θ) 转换为笛卡尔坐标(x,y):
- x = r × cos( θ )
- y = r × sin( θ )
但如果 X 和 Y 是负数呢?
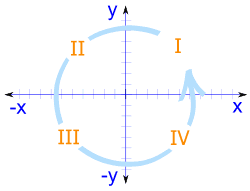
四象限
要考虑负数时,注意到x轴和y轴把平面空间分为
4 个部分:
象限 I、II、III和IV
(逆时钟方向排列)
当由极坐标转换为笛卡尔坐标时这很合适:
例子:(12, 195°) 的笛卡尔坐标是什么?
r = 12 和 θ = 195°
- x = 12 × cos(195°)
x = 12 × -0.9659...
x = −11.59 to 2 decimal places - y = 12 × sin(195°)
y = 12 × -0.2588...
y = −3.11 精确到两位小数
坐标是 (−11.59, −3.11),是在象限 III
可是,当笛卡尔坐标转换为极坐标时。。。。。。
。。。。。。计算器可能会为 tan-1
得到错误的值| 象限 | tan-1的值 |
| I | 用计算器的值 |
| II | 用计算器的值加上 180° |
| III | 用计算器的值加上 180° |
| IV | 用计算器上的值 加上 360° |
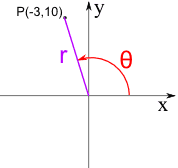
例子:P = (−3, 10)
P 是在象限 II里
- r = √((−3)2 + 102)
r = √109 = 10.4 精确到一位小数 - θ = tan-1(10/−3)
θ = tan-1(−3.33...)
tan-1(−3.33...) 的值是 −73.3°
所以 (−3, 10) 的极坐标是 (10.4, 106.7°)
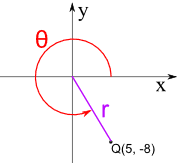
例子:Q = (5, −8)
Q 是在 象限 IV
- r = √(52 + (−8)2)
r = √89 = 9.4 精确到一位小数 - θ = tan-1(−8/5)
θ = tan-1(−1.6)
计算机得到 tan-1(−1.6) 的值是 −58.0°
所以 (5, −8) 的极坐标是 (9.4, 302.0°)
总结
极坐标 (r,θ)转换 为 笛卡尔坐标 (x,y):
- x = r × cos( θ )
- y = r × sin( θ )
笛卡尔坐标 (x,y)转换 为 极坐标 (r,θ):
- r = √ ( x2 + y2 )
- θ = tan-1 ( y / x )
tan-1( y/x ) 可能需要调整:
- 象限 I: 用 计算器的值
- 象限 II: 加 180°
- 象限 III: 加 180°
- 象限 IV: 加 360°
