勾股定理

毕达哥拉斯
2000 多年前有一个关于三角形的神奇发现:
若一个三角形有一个直角,(90°)。。。。。。
。。。。。。而每一边都画一个正方形,。。。。。。
。。。。。。最大的正方形的 面积正好是 其他两个正方形的面积的和!
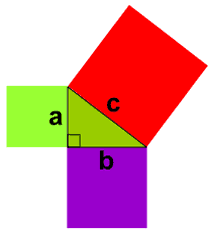
这就是 "毕达哥拉斯定理" 或 勾股定理。一条短短的方程式就可以写出来:
a2 + b2 = c2
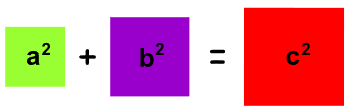
注意:
- c 是 三角形 最长的边
- a 和 b 是 其他两边
定义
直角三角形最长的一边叫 "斜边",所以勾股定理的正式定义是:
在一个直角三角形里:
斜边的平方等于其他两边的平方的和。
真的吗?
我们用个例子来看看。
例子: 一个 "3,4,5" 三角形 有个直角。
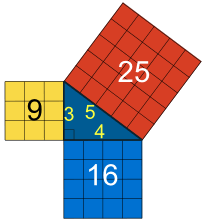 |
我们来看看面积是不是一样的: 32 + 42 = 52 计算后是: 9 + 16 = 25 真的!多奇妙! |

这有什么用?
若我们知到直角三角形 两条边 的长度,我们便可以计算 第三条边的长度。 (但记住,这只适用于直角三角形!)
怎样应用?
以方程式写下来:
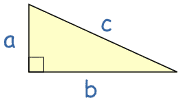 |
a2 + b2 = c2 |
接下来用 代数 来解未知数,像这样:
例子:解这个三角形。
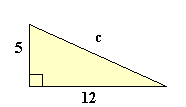 |
a2 + b2 = c2 52 + 122 = c2 25 + 144 = c2 169 = c2 c2 = 169 c = √169 c = 13 |
你也可以去 平方和平方根 学习为什么 √169 = 13
例子:解这个三角形。
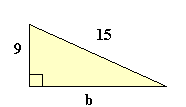 |
a2 + b2 = c2 92 + b2 = 152 81 + b2 = 225 两边减 81: b2 = 144 b = √144 b = 12 |
例子:一个边长是 1 的正方形的 对角线距离 是什么?
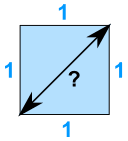 |
a2 + b2 = c2 12 + 12 = c2 1 + 1 = c2 2 = c2 c2 = 2 c = √2 = 1.4142... |
反过来也一样:若三角形的三边符合这条件: a2 + b2 = c2,三角形便是直角三角形
例子:这个三角形有直角吗?
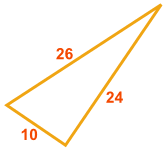 |
这对吗? a2 + b2 = c2
它们相等,所以。。。。。。 对,这个三角形有直角! |
例子: 一个 8, 15, 16 的三角形有直角吗?
82 + 152 = 162 吗?
- 82 + 152 = 64 + 225 = 289,
- 但 162 = 256
所以,不,这个三角形没有直角
例子:这个三角形有直角吗?
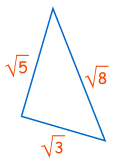 |
这对吗? a2 + b2 = c2 (√3)2 + (√5)2 = (√8)2 吗?
3 + 5 = 8 吗?
当然! 这个 是 直角三角形 |
你可以自己证明这个定理!
拿纸、笔和剪刀,然后按这动画去做:
- 在纸上画一个直角三角形,周围多留些空间。
- 在斜边(最长的一边)上画一个正方形
- 在斜边的另一边画同样大小的正方形
- 按动画的指示画线,像这样:

- 剪下图形
- 把图形拼起来,看看可不可以证明大的正方形的面积是另外两个正方形的总和
另外一个非常简单的证明
这里有一个很古老的证明。
看动画时,留心三角形是怎样移动的。
你可能要多看几次才会明白。
最重要的是紫色的三角形。
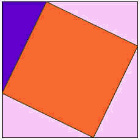 |
变成 | 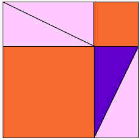 |
这个证明如何 把面积加起来。
| 历史附注: 在西方,这个定理叫毕达哥拉斯定理,但印度、希腊、中国和巴比伦的数学家都在毕达哥拉斯在世以前很久已熟悉这个定理! |