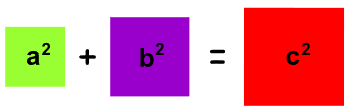勾股数
"勾股数" 是一组三个正 整数,a、b 和 c,而且这三个数符合这个规则:
a2 + b2 = c2
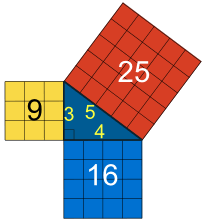
例子: 最小的勾股数是 3、4 和 5。
我们来验证:
32 + 42 = 52
计算出来是:
9 + 16 = 25
是对的
三角形
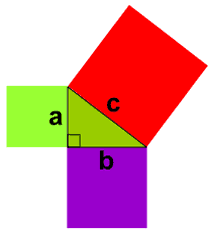 |
有勾股数的三角形是 直角三角形 (去 勾股定理 了解更多):
注意:
|
例子: 勾股数 3、4 和 5 形成一个 直角三角形

再看几个例子:
| 5, 12, 13 | 9, 40, 41 |
 |
 |
| 52 + 122 = 132 | 92 + 402 = 412 |
| 25 + 144 = 169 | (自己来试试看) |
每个三角形都有直角!
最初的几个
以下是最初的几个勾股数(不 包括以下数中 "按比例增大" 的):
| (3,4,5) | (5,12,13) | (7,24,25) | (8,15,17) | (9,40,41) |
| (11,60,61) | (12,35,37) | (13,84,85) | (15,112,113) | (16,63,65) |
| (17,144,145) | (19,180,181) | (20,21,29) | (20,99,101) | (21,220,221) |
| (23,264,265) | (24,143,145) | (25,312,313) | (27,364,365) | (28,45,53) |
| (28,195,197) | (29,420,421) | (31,480,481) | (32,255,257) | (33,56,65) |
| (33,544,545) | (35,612,613) | (36,77,85) | (36,323,325) | (37,684,685) |
| 。。。。。。 还有无限多。。。。。。 | ||||
按比例增大
最容易创造更多勾股数的方法是把已知的勾股数按比例增大。
例子:把 3、4、5 按比例增大一倍,成为 6、8、10
这三个数也符合公式 a2 + b2 = c2:
62 + 82 = 102
36 + 64 = 100
想了解更多?去看 勾股数――高级