勾股数――高级
"勾股数"是符合以下规则的一组整数, a、b 和 c:
a2 + b2 = c2
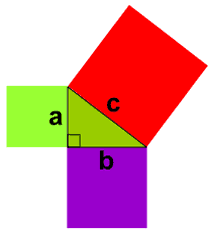
三角形
若三角形的边长是 a、b 和 c,则三角形是直角三角形(去浏览勾股定理了解更多):
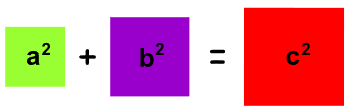
注意:
- c 是 三角形最长的边,叫 "斜边"(也叫弦)
- a 和 b 是两条直角边。(短的叫勾,长的叫股)
勾股数
勾股数例子:
| 3, 4, 5 | 5, 12, 13 | 9, 40, 41 |
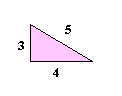 |
 |
 |
| 32 + 42 = 52 | 52 + 122 = 132 | 92 + 402 = 412 |
| 9 + 16 = 25 | 25 + 144 = 169 | (自己试试看!) |
无穷
有无穷多的勾股数。
我们可以用第一个勾股数组(3、4 和 5)来证明:
若 n 为大于 1 的整数,则 3n、4n 和 5n 也是一个勾股数组。因为:
(3n)2 + (4n)2 = (5n)2
例子:
| n | (3n, 4n, 5n) | |
|---|---|---|
| 2 | (6,8,10) | |
| 3 | (9,12,15) | |
| ... | …… 等 …… |
所以我们可以用(3、4、5)来生成无穷多的勾股数。
有无穷多的勾股数――欧几里得的证明
欧几里得用另一个方法来证明有无穷多的勾股数。
这个证明是基于:两个连续的数的平方的差必然是个奇数
例子:
22 − 12 = 4−1 = 3(奇数),
152 − 142 = 225−196 = 29(奇数)
每个奇数都等于两个连续的数的平方的差。看看这个列表:
| n | n2 | 差 | ||
|---|---|---|---|---|
| 1 | 1 | |||
| 2 | 4 | 4−1 = 3 | ||
| 3 | 9 | 9−4 = 5 | ||
| 4 | 16 | 16−9 = 7 | ||
| 5 | 25 | 25−16 = 9 | ||
| …… | …… | …… |
我们知道有无穷多的奇数,并且奇平方数是奇数的子集,而无穷大的一部分还是无穷大,所以也有无穷多的奇平方数。因此,也有无穷多的勾股数。
属性
趣事:每组勾股数:
- 全都是偶数,或者
- 是两个奇数和一个偶数。
一个勾股数组不能全是奇数,也不能是两个偶数和一个奇数。因为:
- 奇数的平方是奇数,偶数的平方是偶数。
- 两个偶数的和是偶数,偶数与奇数的和是奇数。
因此,若 a 和 b 都是偶数,则 c 也是偶数。同样,若 a 和 b 其中一个是奇数而另一个是偶数,c 便必然是奇数!
求勾股数
求勾股数其实很容易。
设 m 和 n 为任何不同的正整数(m < n):
- a = n2 − m2
- b = 2nm
- c = n2 + m2
则 a、b 和 c 是勾股数。
例子:m=1、n=2
- a = 22 - 12 = 4 − 1 = 3
- b = 2 × 2 × 1 = 4
- c = 22 + 12 = 5
我们得到第一组勾股数(3、4、5).
当 m=2、n=3 时,结果就是下一组勾股数(5、12、13)。
前几组勾股数
这是所有 a、b、c 都小于 1,000 的勾股数
这里只列出第没有公因数的勾股数(叫素勾股数),所以(a、b、c)的倍数,例如(2a、2b、2c)和(3a、3b、3c)等等都没有列出来。
例子:(3、4、5)是勾股数。(6、8、10)也是,但不在列表里,因为它只不过是(3、4、5)乘 2.
| (3,4,5) | (5,12,13) | (7,24,25) | (8,15,17) | (9,40,41) |
| (11,60,61) | (12,35,37) | (13,84,85) | (15,112,113) | (16,63,65) |
| (17,144,145) | (19,180,181) | (20,21,29) | (20,99,101) | (21,220,221) |
| (23,264,265) | (24,143,145) | (25,312,313) | (27,364,365) | (28,45,53) |
| (28,195,197) | (29,420,421) | (31,480,481) | (32,255,257) | (33,56,65) |
| (33,544,545) | (35,612,613) | (36,77,85) | (36,323,325) | (37,684,685) |
| (39,80,89) | (39,760,761) | (40,399,401) | (41,840,841) | (43,924,925) |
| (44,117,125) | (44,483,485) | (48,55,73) | (48,575,577) | (51,140,149) |
| (52,165,173) | (52,675,677) | (56,783,785) | (57,176,185) | (60,91,109) |
| (60,221,229) | (60,899,901) | (65,72,97) | (68,285,293) | (69,260,269) |
| (75,308,317) | (76,357,365) | (84,187,205) | (84,437,445) | (85,132,157) |
| (87,416,425) | (88,105,137) | (92,525,533) | (93,476,485) | (95,168,193) |
| (96,247,265) | (100,621,629) | (104,153,185) | (105,208,233) | (105,608,617) |
| (108,725,733) | (111,680,689) | (115,252,277) | (116,837,845) | (119,120,169) |
| (120,209,241) | (120,391,409) | (123,836,845) | (124,957,965) | (129,920,929) |
| (132,475,493) | (133,156,205) | (135,352,377) | (136,273,305) | (140,171,221) |
| (145,408,433) | (152,345,377) | (155,468,493) | (156,667,685) | (160,231,281) |
| (161,240,289) | (165,532,557) | (168,425,457) | (168,775,793) | (175,288,337) |
| (180,299,349) | (184,513,545) | (185,672,697) | (189,340,389) | (195,748,773) |
| (200,609,641) | (203,396,445) | (204,253,325) | (205,828,853) | (207,224,305) |
| (215,912,937) | (216,713,745) | (217,456,505) | (220,459,509) | (225,272,353) |
| (228,325,397) | (231,520,569) | (232,825,857) | (240,551,601) | (248,945,977) |
| (252,275,373) | (259,660,709) | (260,651,701) | (261,380,461) | (273,736,785) |
| (276,493,565) | (279,440,521) | (280,351,449) | (280,759,809) | (287,816,865) |
| (297,304,425) | (300,589,661) | (301,900,949) | (308,435,533) | (315,572,653) |
| (319,360,481) | (333,644,725) | (336,377,505) | (336,527,625) | (341,420,541) |
| (348,805,877) | (364,627,725) | (368,465,593) | (369,800,881) | (372,925,997) |
| (385,552,673) | (387,884,965) | (396,403,565) | (400,561,689) | (407,624,745) |
| (420,851,949) | (429,460,629) | (429,700,821) | (432,665,793) | (451,780,901) |
| (455,528,697) | (464,777,905) | (468,595,757) | (473,864,985) | (481,600,769) |
| (504,703,865) | (533,756,925) | (540,629,829) | (555,572,797) | (580,741,941) |
| (615,728,953) | (616,663,905) | (696,697,985) |
 |