活动:沙漠步行

摔机!
翠翠在沙漠摔机着陆了。
附近有个村落,不过不知到在哪个方向。
翠翠想到一个巧妙的计划:
- 从飞机拿一瓶水和一个罗盘 ,
- 然后向北走 1 km,转方向,向东走 2 km,再向南 3 km,向西 4 km,向北 5 km,向东 6 km,。。。像这样:
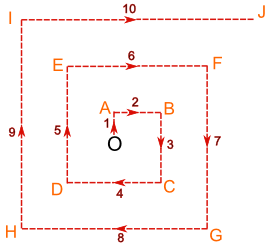
这样无论目前在哪个方向,她一定会找到村落,还(希望)可以回到飞机去拿水,如需要的话。
但走完每个阶段,她需要知道:
- 她总共走了多远
- 回到飞机的直线距离有多远
好,我们来算算……
走完旅程的第一的阶段,翠翠来到
A 点:
- 她走了 1 km。
- 她跟飞机的直线距离是 1 km。
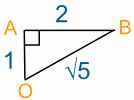
两个阶段后,她来到
B点:
- 她总共走了 3 km。
- 回答第二个问题,我们画个直角三角形 OAB:
三阶段后,他到达 C 点:
该你来做了!
填上数值……如果有困难,到下面看看
| 点 | 总共走的 距离 |
距离
O
的直线距离 |
|---|---|---|
| O | 0 | 0 |
| A | 1 | 1 |
| B | 3 | √5 |
| C | 6 | |
| D | ||
| E | ||
| F | ||
| G | ||
| H | ||
| I | ||
| J |
比较容易的方法
总共走的距离
走完每一个阶段,总距离是这序列 1 + 2 + 3 + 4 + 5 + 6 + ……的和
所以你可以每次加上新的距离。
或 你可以这样计算:
n(n
+ 1)/2
,其中
n
是阶段的数目。
像这样:
| 阶段的 数目 (n) |
总共走的距离 = n(n + 1)/2 |
| 1 | 1 × 2 / 2 = 1 |
| 2 | 2 × 3 / 2 = 3 |
| 3 | 3 × 4 / 2 = 6 |
| 4 | 依此类推 |
这叫 "三角形数序列":
尝试用这两种方法来计算。
离 O 的直线距离
要计算回到飞机的距离,我们可以在 坐标格网 上画下步行路线,像这样:
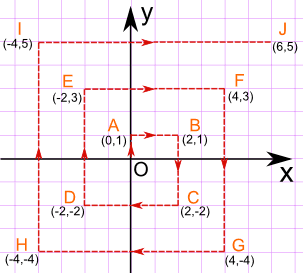
接下来我们只不过是要求 两点之间的距离
这两点 (xA,yA) 和 (xB,yB) 之间的距离由下式给出:
![]()
两点其中的一点一定是原点 (0,0), 所以当 xB and yB 是零, 我们得到:
![]()
例如,点 E (-2, 3), x = -2 和 y = 3,所以:
![]()
希望这会对你有帮助。
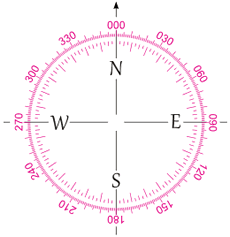
方向?
翠翠还要知道一件事:要回到飞机,她要朝罗盘的哪个方位走?
我们会在 活动:沙漠步行 2 探索这个