两点之间的距离
这是怎样计算两个已知坐标点之间的距离:
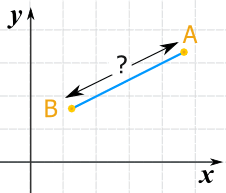
把两点名为 A 和 B
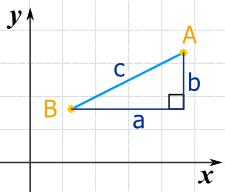
我们用从 A 画的垂直线和从 B 画的水平线,形成一个直角三角形。
勾股定理告诉我们:
a2 + b2 = c2
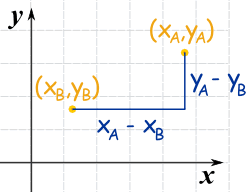
标出 A 和 B的坐标。
xA 代表 A 的 x坐标
yA 代表 A 的 y坐标
水平距离 a 是 (xA − xB)
垂直距离 b 是 (yA − yB)
我们现在可以解 c (两点之间的距离):
| 开始: | c2 = a2 + b2 | |
| 代进 a 和 b 的式: | c2 = (xA − xB)2 + (yA − yB)2 | |
| 结果: |
例子:
例子 1
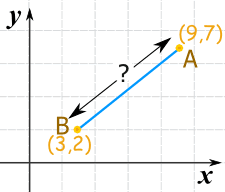
| 代入值: | ||
例子 2
两点的次序并不重要,因为取平方会把负数变成正数:
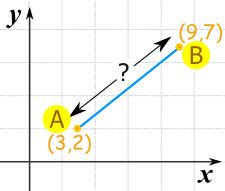
| 代入值: | ||
例子 3
这例子有负坐标……但同样计算:
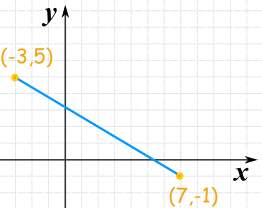
| 代入值: | ||
(注意: √136 可以再简化为 2√34)
三维或更高维数
三维(或更高维数)都是一样的!
取两点在每条轴的差的平方,再把结果加起来,最后取和的平方根:
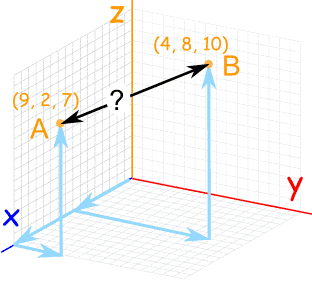
(9,2,7) 和 (4,8,10)的距离是:
![c = [(9-4)^2+(2-8)^2+(7-10)^2]的平方根 70的平方根 = 8.37……](images/dist-2-points-3d-equn.gif)