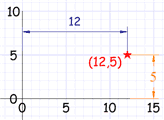
从两点找线的方程
怎样计算
如果我们知道两点,我们便可以算出经过它们的直线的方程。
这是一个示范。尝试拖动那些点看看。
我们现在来看怎样算出方程。首先,我们要找坡度。。。。。。
从两点找坡度(斜率)
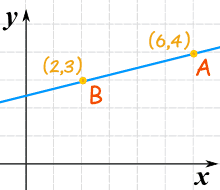 |
这条线的坡度(斜率)是什么?我们有两点:
|
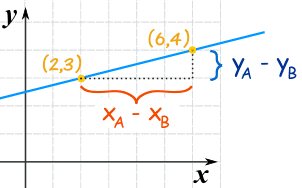
坡度是高度的改变除以水平距离的改变。
|
。。。。。。公式是: 坡度 m = y 的改变x 的改变 = yA − yBxA − xB |
所以我们:
- 计算Y值的差,
- 计算X值的差
- 相除
像这样:
m = y 的改变 x 的改变 = 4−3 6−2 = 1 4 = 0.25
无论哪点放在前面,结果都是一样的。试试把点对调:
m = y 的改变 x 的改变 = 3−4 2−6 = −1 −4 = 0.25
已知两点求方程
我们计算了坡度,现在我们可以求整个方程。
 |
这条线的方程是什么?
|
最简单的方法是从"点斜式" 开始:
y − y1 = m(x − x1)
我们可以用线上任何一点为 "1",我们就用 (2, 3)这点:
y − 3 = m(x − 2)
用上面的坡度的公式来计算 "m":
坡度 m = y 的改变x 的改变 = 4−36−2 = 14
我们得到:
y − 3 = (1/4)(x − 2)
这答案没错,但我们可以再把它简化:
y − 3 = x/4 − 2/4
y = x/4 − ½ + 3
y = x/4 + 5/2
这叫"斜截式 (y = mx + b)"。
检测!
我们用第二点 (6, 4) 来检测:
y = x/4 + 5/2 = 6/4 + 2.5 = 1.5 + 2.5 = 4
对了,当 x=6,y=4,所以答案是对的!
另一个例子
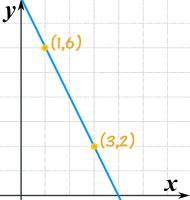 |
这条线的方程是什么?
|
从"点斜式" 开始:
y − y1 = m(x − x1)
代入这些值:
- x1 = 1
- y1 = 6
- m = (2−6)/(3−1) = −4/2 = −2
我们得到:
y − 6 = −2(x − 1)
我们可以把它变为"斜截式 (y = mx + b)":
y − 6 = −2x + 2
y = −2x + 8
重要的例外
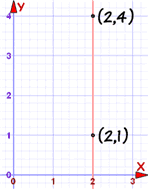
上面的方法好使,但有一个特别情况不适用:垂直线:
|
垂直线的斜率是未定义的(因为我们不能除以零): m = yA − yBxA − xB = 4 − 12 − 2 = 30 = 未定义 但我们仍然可以写这个方程:用 x=,而不用 y=,像这样: x = 2 |