直线方程的点斜式
直线方程的"点斜"式是:
y − y1 = m(x − x1)
当我们知道:
我们可以用这公式来找直线上其他的点。
它代表什么?
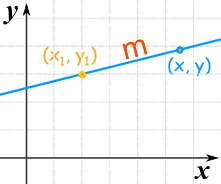
(x1, y1) 是 已知点
m 是直线的 坡度
(x, y) 是直线上任何其他一点
来了解它
这公式是基于坡度的:
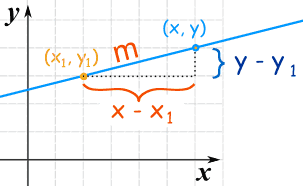
坡度 m = y 的改变 x 的改变 = y − y1 x − x1
从坡度开始: 这样重排:
变成这样: |
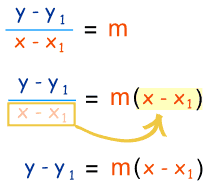 |
这只不过是坡度的公式的另一种表达方式!
现在我们来看看怎样应用这种形式。
例子:
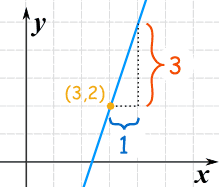
坡度 "m" = 31 = 3
y − y1 = m(x − x1)
我们知道 m,也知道 (x1, y1) = (3,2),所以:
y − 2 = 3(x − 3)
答案没错,但我们可以再简化一点:
y − 2 = 3x − 9
y = 3x − 9 + 2
y = 3x − 7
例子 2:
m = −3 1 = −3
y − y1 = m(x − x1)
我们可以任意选一点为 (x1, y1),我们这里选 (0,0):
y − 0 = −3(x − 0)
简化成:
y = −3x
例子 3: 垂直线
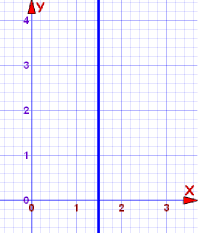 |
垂直线的方程是什么?
坡度是未定义的!
这是个特例,我们用另一个方程:
x = 1.5
这条线上的每一点都符合 x坐标为 1.5,
所以方程是 x = 1.5
用这个 y = mx + b 呢?
你可能已经熟悉 "y=mx+b" 的直线方程形式。
其实这是同一个方程,不过以不同形式来表达!
"b" 的值(叫Y截距)是直线与Y轴相交的地方。
所以 (x1, y1) 这点其实是在 (0, b)
方程改写:
| 开始: | y − y1 = m(x − x1) |
| (x1, y1) 其实是 (0, b): | y − b = m(x − 0) |
| 就是: | y − b = mx |
| 把 b 换边: | y = mx + b |
这就是直线方程的 "斜截"式。