活动:沙漠步行 2
怎样知道向哪个 方向 走
摔机!
 如果你还不认识翠翠,你应该先去做 沙漠步行 这个活动。
如果你还不认识翠翠,你应该先去做 沙漠步行 这个活动。
翠翠在沙漠摔机着陆了,但她想到一个巧妙的计划去找最近的村落:
- 从飞机拿
一瓶水和一个罗盘,
- 然后向北走 1 km, 转方向, 向东走 2 km,再向南 3 km,向西 4 km,向北 5 km,向东 6 km,……像这样:
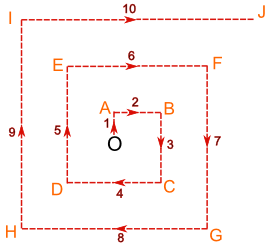
这样无论目前在哪个方向,她一定会找到村落,还(希望)可以回到飞机去拿水,如需要的话。
- 先从北方计量
- 顺时针方向计量
- 计量方位到三位(或多过三位,如果有小数点)
可是,如果她找不到村落,每隔数小时她需要回到飞机去休息和拿水。
活动:沙漠步行计算了步行的距离。
现在我们来寻找 方向。
从 A 点回到飞机她只需折会重走,所以她向南走。
如果她在 B 点呢? 她要向哪个方向走才能回到飞机?
我们以前看过这三角形:
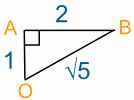
我们计算了距离 OB = √5 km
要找方向,我们需要计算一个 角度, 像角度 ABO,在以下的图标志为 θ:
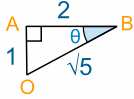
找角度 θ 的大小,我们需要用 三角法
我们知到三边的长度,但用整数比较容易,所以我们用对边 AO = 1 和邻边 AB = 2. SOHCAHTOA 告诉我们去用切线 (Tangent):
在计算器上摁 tan-1 鈕或 atan 钮:
角度是 26.6°
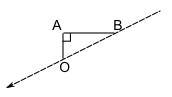
那是什么方向?
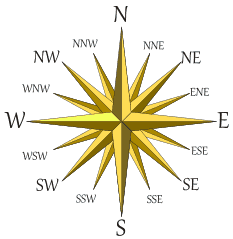 |
这角度是在南与西之间,较近西。 就叫西南偏西吧。 可是这不太准确。翠翠回不到飞机了! 在这情况下可能不重要,因为 B 离飞机不远,她可能可以看到飞机。 但是在其他地方就需要准确很多了. |
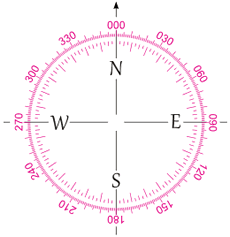 |
我们要用 三位方位角。 什么是三位方位角?三位方位角是比罗盘方位准确很多的另外一个表达方向的方法,它有独特的计量方法:
飞行员和舵手用三位方位角。 |
例子
东、南、西、北四个主要方向是 90° 的倍数:
东是 090° 而不是 90° 因为要用三位数字。
三位方位角的好处是每一个方向都有独特的描述:
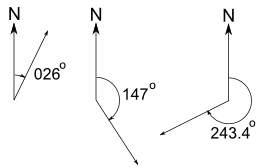
最后那个有四位数字(小数点前三个,小数点后一个),但这仍叫三位方位角, .4 部分只是更准确。
现在来比较这例子和翠翠回飞机(O)需要走的方向:
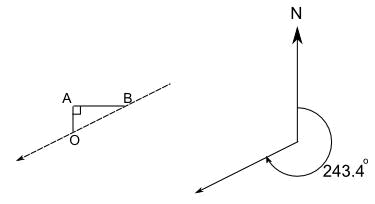
两个方向是一样的 243.4° 和 我们刚才得到的 26.6° 有什么关系?
这很容易: 270° - 26.6° = 243.4°
轮到你了
你可以开始填下面的列表,填到 E 点 (我们将会用另一个方法来算点 F 到 J)。
(注意:距离是在 沙漠步行里计算的)。
用直角三角形来帮你计算翠翠需要走回飞机(O)的方向的三位方位角:
| 点 | 总共走的 距离 |
距离
O 的 直线距离 |
回到
O 到 三位方位角 |
| O | 0 | 0 | 不适用 |
| A | 1 | 1 | 180° |
| B | 3 | √5 | 243.4° |
| C | 6 | ||
| D | |||
| E |
用极坐标
在 沙漠步行中,我们用 笛卡儿坐标 来计算从 O 的直线距离:
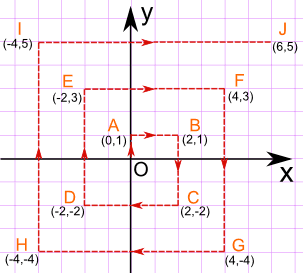
用 笛卡儿坐标 表示一点,你用点向右和向上的距离:
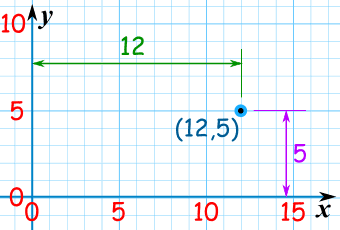
但是你也可以用另一个坐标,叫 极坐标。
用 极坐标 形容一点,你用离原点的距离和角度:
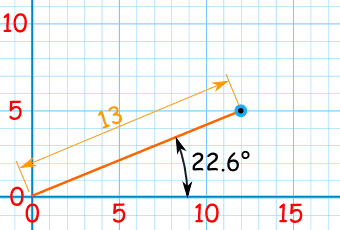
在笛卡儿坐标, (12, 5) 这点与在极坐标的 (13, 22.6°) 这点是同一点。
我们就是要这样!翠翠需要走的 距离 和 方向 。
从笛卡儿坐标的 (x,y) 转变为极坐标的 (r,θ):
r = √( x2 + y2 )
θ = tan-1 ( y / x )
我们来再计算 B 点。 x = 2 和 y = 1,所以:
r = √( x2 + y2 )= √( 22 + 12 )= √( 4 + 1 )= √5
θ = tan-1 ( y / x ) = tan-1 ( 1/2 ) = 26.6°
B 点的极坐标是 (√5, 26.6°)
但三位方位角究竟是什么?
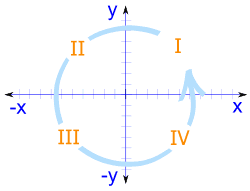 |
基于点所在的 象限 ,有一条简单的规则:
|
B 点 (在象限 I), θ = 26.6°,三位方位角是 270° - 26.6° = 243.4°
再做另一点:I 点, x= -4 和 y = 5,所以:
r = √( x2 + y2 )= √( (-4)2 + 52 )= √( 16 + 25 )= √41
θ = tan-1 ( y / x ) = tan-1 ( 5/-4 ) = tan-1 (-1.25) = 128.7°
I 是在象限 II,所以三位方位角是 270° - 128.7° = 141.3°
你现在应该可以完成以下的列表了:
| 点 | r 的值 | θ 的值 | 极坐标 | 回到
O 的 三位方位角 |
| O | 0 | 0° | (0, 0°) | 不适用 |
| A | 1 | 90° | (1, 90°) | 180° |
| B | √5 | 26.6° | (√5, 26.6°) | 243.4° |
| C | ||||
| D | ||||
| E | ||||
| F | ||||
| G | ||||
| H | ||||
| I | √41 | 128.7° | (√41, 128.7°) | 141.3° |
| J |
