四象限里的正弦、余弦和正切
正弦、余弦和正切
三角法里的三个主要函数是正弦、余弦和正切。
算法很简单:
把三角形的
一边除以另外一边
……但我们必须知道是哪一边!
以 θ 为角度,这些函数的计算方法是:
正弦函数: |
sin(θ) = 对边 / 斜边 |
余弦函数: |
cos(θ) = 邻边 / 斜边 |
正切函数: |
tan(θ) = 对边 / 邻边 |
例子:35°的正弦是多少?
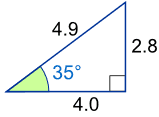 |
用这个三角形(长度准确到一个小数位): sin(35°) = 对边 / 斜边 = 2.8/4.9 = 0.57…… |
笛卡尔坐标
在笛卡尔坐标里,我们用左右 和 上下 的距离来表达一个点:
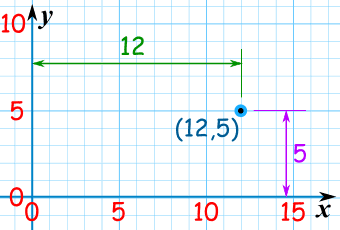
点 (12,5) 是向右 12 单位,和向上 5 单位。
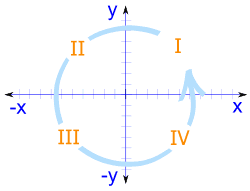
四个象限
包括负数在内,x轴 和 y轴把平面空间分成四个部分:
象限 I、II、III 和 IV
(以逆时针方向排序)
- 在象限 I,x 和 y 两者皆为正数,
- 在象限 II ,x 是负数(y 仍是正数),
- 在象限 III x 和 y 两者皆为负数,
- 在象限 IV,x 再次是正数,而 y 是负数。
如下:
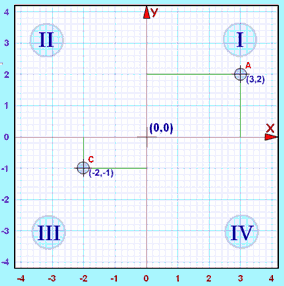
| 象限 | X (水平) |
Y (垂直) |
例子 |
|---|---|---|---|
| I | 正 | 正 | (3,2) |
| II | 负 | 正 | |
| III | 负 | 负 | (−2,−1) |
| IV | 正 | 负 |
例子:点 "C"(−2,−1)是在负(向左)2 单位和负(向下)1单位。
x 和 y 两者都是负数,所以点是在 "象限 III"
四个象限里的正弦、余弦和正切
现在我们来看看在每个象限的 30°三角形。
在象限 I,一切正常, 正弦、余弦和正切 全是正数:
例子:30°的正弦、余弦和正切
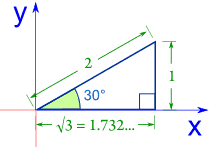
正弦 |
sin(30°) = 1 / 2 = 0.5 |
余弦 |
cos(30°) = 1.732 / 2 = 0.866 |
正切 |
tan(30°) = 1 / 1.732 = 0.577 |
但在象限 II,x 是负数,余弦和正切也变成负数:
例子:150°的正弦、余弦和正切
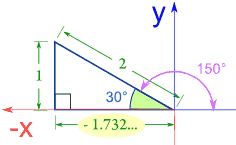
正弦 |
sin(150°) = 1 / 2 = 0.5 |
余弦 |
cos(150°) = −1.732 / 2 = −0.866 |
正切 |
tan(150°) = 1 / −1.732 = −0.577 |
在象限 III,正弦和余弦是负数:
例子:210°的正弦、余弦和正切
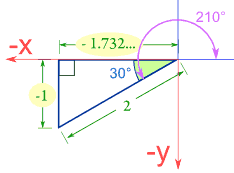
正弦e |
sin(210°) = −1 / 2 = −0.5 |
余弦 |
cos(210°) = −1.732 / 2 = −0.866 |
正切 |
tan(210°) = −1 / −1.732 = 0.577 |
注意:正切是正数,因为负数除以负数的结果是正数。
In 象限 IV,正弦和正切是负数:
例子:330°的正弦、余弦和正切
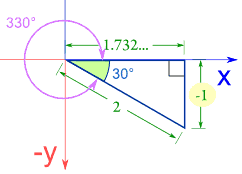
正弦 |
sin(330°) = −1 / 2 = −0.5 |
余弦 |
cos(330°) = 1.732 / 2 = 0.866 |
正切 |
tan(330°) = −1 / 1.732 = −0.577 |
有个规律!看看正弦、余弦和正切在什么地方是正数……
- 在象限 I,三个函数都是正数
- 在象限 II,只有正弦是正数
- 在象限 III,只有正切是正数
- 在象限 IV,只有余弦是正数
在这图可以看得很清楚:
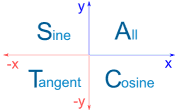
| 你可以记着英语字母 ASTC,就是 (A)ll(全部)、(S)ine、(T)angent 和 (C)osine。 | 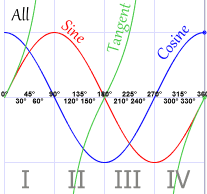 这图也显示 "ASTC"。 |
两个值
看这个正弦的图:
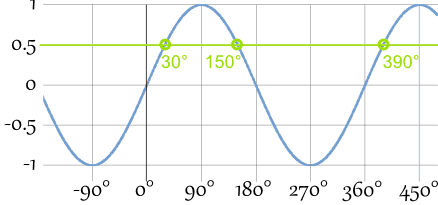
(在头 360°里),有 两个角度的正弦是相同的!
余弦 和 正切也一样。
麻烦的是:计算器只会给你其中一个答案……
……但你可以用以下的规则来求另一个答案:
| 第一值 | 第二值 | |
| 正弦 | θ | 180º − θ |
| 余弦 | θ | 360º − θ |
| 正切 | θ | θ − 180º |
若角度小于 0º,加 360º.
我们现在可以解方程在 0º 与 360º之间的答案了(用 反正弦、反余弦和反正切)
例子:解 sin θ = 0.5
用计算器,我们得到第一个答案 = sin-1(0.5) = 30º (在象限 I)
另一个答案是 180º − 30º = 150º ((象限 II)
例子:解 tan θ = −1.3
用计算器,我们得到第一个答案 = tan-1(−1.3) = −52.4º
这是小于 0º,所以加 360º:−52.4º + 360º = 307.6º (象限 IV)
另一个答案是 307.6º − 180º = 127.6º (象限 II)
例子:解 cos θ = −0.85
用计算器,我们得到第一个答案 = cos-1(−0.85) = 148.2º (象限 II)
另一个答案是 360º − 148.2º = 211.8º (象限 III)