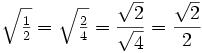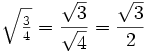单位圆
"单位圆" 是半径为 1 的圆。
单位圆非常简单,所以用来学习长度和角很合适。
圆心放在图上 x轴和 y轴的交点。
正弦、余弦和正切
因为半径是 1,我们可以直接测量正弦、余弦和正切的值。
如果角 θ是 0°呢?
cos 0° = 1、sin 0° = 0、tan 0° = 0
如果角 θ是 90°呢?
cos 90° = 0、sin 90° = 1、tan 90°是未定义
自己来试试!
自己来试试!移动鼠标来看不同的角(以弧度 或 角度为单位)对正弦、余弦和正切的影响
在笛卡尔坐标里, "角边" 可以是正数或负数,因此,正弦、余弦和正切也可以是正数或负数.
也去玩玩互动单位圆。
勾股
勾股定理说明:在直角三角形里,斜边的平方等于另外两边的平方的和:
x2 + y2 = 12
但 12 是 1,所以:
x2 + y2 = 1
(单位圆的方程)
因为 x=cos 和 y=sin,我们得到:
(cos(θ))2 + (sin(θ))2 = 1
一个有用的 "恒等式"
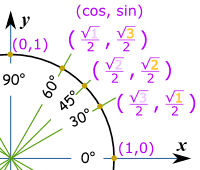
重要的角:30°、45° 和 60°
你应该尝试牢记这些角度的正弦、余弦和正切的值:30°、45° 和 60°。
要牢记东西可能有点辛苦,但这会对你在考试或需要做快速运算的时候很有帮助。
牢记这些!
| 角度 | 正弦 | 余弦 | 正切=正弦/余弦 |
|---|---|---|---|
| 30° | 1 √3 = √3 3 | ||
| 45° | 1 | ||
| 60° | √3 |
怎样去记?
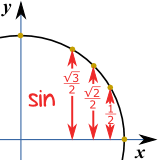
这样想: "1、2、3" :
| sin(30°) = | √1 | = | 1 | (because √1 = 1) | |
| 2 | 2 |
| sin(45°) = | √2 | |
| 2 |
| sin(60°) = | √3 | |
| 2 |
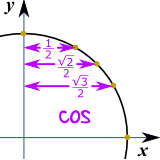
余弦(cos)就是 "3, 2, 1"
| cos(30°) = | √3 | |
| 2 |
| cos(45°) = | √2 | |
| 2 |
| cos(60°) = | √1 | = | 1 | (because √1 = 1) | |
| 2 | 2 |
只要记住三个数
| 只要记住三个数就够了: | 1 | , | √2 | and | √3 |
| 2 | 2 | 2 |
因为余弦和正弦都是这三个数:
 |
 |
正切呢?
正切 = 正弦/余弦,所以我们可以这样做:
|
但写 1/√3 可能会扣分 (见有理分母),所以应该这样写:√3/3 |
|||||||||||||
|
||||||||||||||
|
画个草图
画个草图也可以帮你记住 30° 和 60°:
| 画一个边长为 2的三角形 | 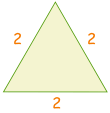 |
|
|
把三角形一分为二。勾股定理说新的边的长度是 √3 12 + (√3)2 = 22
1 + 3 = 4 |
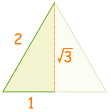 |
|
| 然后用正弦、余弦和正切的定义来记 | 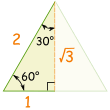 |
例子:sin(30°)
正弦:
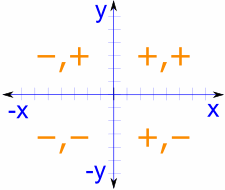
全圆
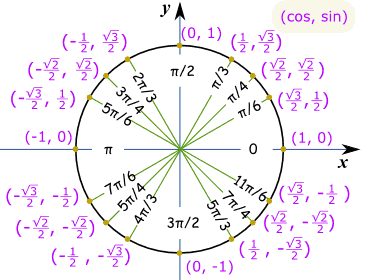
要知道全圆里的正弦和余弦的值,我们需要覆盖每一个象限,并且根据笛卡尔坐标加上正确的正负号:
注意我们先写余弦(cos),再写正弦(sin),所以就是(余弦,正弦):
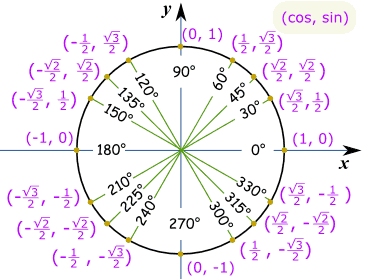
例子:cos(330°) 是多少??
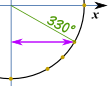
| 画个草图,我们可以看到答案是 "长" 的值: | √3 |
| 2 |
这是同一个单位圆,不过角的单位是弧度。
例子:sin(7π/6) 是多少?
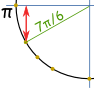
想: "7π/6 = π + π/6",然后画草图。
我们可以看到答案是负数,是 "短" 的值:−½
脚注:这些值是怎样计算出来的?我们可以用方程 x2 + y2 = 1 来求 x 和 y 的长度(当半径等于 1 时,答案是 cos 和 sin):
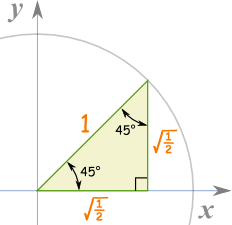
45度45度:x 与 y 相等,所以 y=x: x2 + x2 = 1
2x2 = 1
x2 = ½
x = y = √(½)
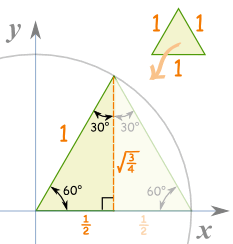
60度把一个等边三角形 (所有边等长,所有角是 60°)在中间一分为二。 "x" 边变成 ½, "y" 边是: (½)2 + y2 = 1
¼ + y2 = 1
y2 = 1-¼ = ¾
y = √(¾)
30度30°就是 x 和 y 对调了的 60°,所以 x = √(¾),y = ½ 并且:
结果是(和上面一样):
|