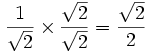把分母化为有理数
 |
"把分母化为有理数" 是把一个方根（像平方根 或 立方根）从一个分数的下面移到上面。 |
糟了！无理的分母！
分数下面的部分叫分母。
像 2 和 3 的数叫 有理数。
但很多方根，例如 √2 和 √3，是 无理数。
例子：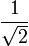
的分母是无理数。
在其"最简单"的形式，分数是没有无理的分母的！
修补（把分母化为有理数）
便是 "把分母化为有理数"
注意：无理分母并不是错的，不过它不是"最简单"的形式，所以老师可能会扣分。
把无理数从分母移除也会帮助你解方程，所以学会这个运算是有用的。
怎样做？
一、把上面和下面乘以一个方根
有时只需把上面和下面乘以一个方根：
注意：分数的上面（分子）可以含有无理数。
二、把上面和下面乘以共轭
还有一个特别的方法来把平方根从分数的下面移到上面……把上面和下面乘以分母的 共轭。
共轭是把两个项中间的正负号倒转的结果：
| 例式 | 共轭 | |
|---|---|---|
| x2 − 3 | x2 + 3 |
| 例式 | 共轭 | |
|---|---|---|
| a + b3 | a − b3 |
这个很管用，因为把一个式子与其共轭相乘会得到平方项，像这样：
做法：
例子：这是有"无理分母"的分数：
怎样把2的平方根移到上面？
答案：把上面和下面乘以3−√2 的共轭（这不会改变分数的值）：
（留意到我们在分母上用了这个公式 吗？）
有用！
把这个记住着，将来可能有用！