三角法入门
英语 Trigonometry (源自希腊语 trigonon: "triangle(三角)" + metron: "measure(测量)")
有兴趣学习三角法吗?这是一个简单的摘要。
请浏览以下链接或去三角索引看看
 |
三角法……是关于三角形的学问。 |
三角法帮助我们求角度和距离。在很多不同的领域,例如科学、工程、电玩等等,三角法都大有用场!
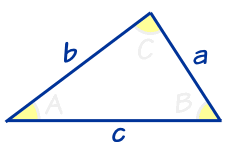
直角三角形
最重要的三角形是 直角三角形。在角落的小正方形便是代表那个角是个直角:
另外一个角通常是标志为 θ,三条边的名字是:
- 邻边:在角 θ 的旁边
- 对边:在角 θ 的对面
- 斜边:最长的边
正弦、余弦和正切
我们可以用三角法来求一条边的长度或一个角的角度。常用的函数是正弦、余弦和正切。
这些函数只不过是三角形一边的长度除以另一边的长度。
对一个角 "θ":
(正弦、余弦和正切通常被简写为 sin、cos 和 tan。)
例子:35°的正弦是多少?
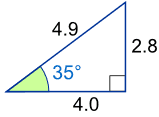 |
用这个三角形(长度精确到一位小数): sin(35°) = 对边 / 斜边 = 2.8/4.9 = 0.57…… |
计算器有 sin、cos 和 tan 的功能,我们来看看怎样使用:
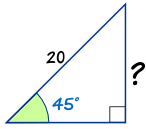
例子:未知的长度是多少?
- 我们知道 斜边
- 我们想求 对边
正弦 是 对边 / 斜边 的比:
sin(45°) = 对边 斜边

把 "45" 打入计算器,然后按 "sin" 键:
sin(45°) = 0.7071……
现在我们知道:
0.7071…… = 对边 20
我们用代数来解。先换边:
对边 20 = 0.7071……
每边乘以 20 (斜边的长度):
| 对边e | = 0.7071…… × 20 |
| = 14.14 (保留两位小数) |
做好了!
来试试正弦、余弦和正切
移动鼠标来看看不同点角度对正弦、余弦和正切有什么影响:
请留意,基于笛卡尔坐标的规矩,边长可以是正数或负数。故此,正弦、余弦和正切的值也会是正数或负数。
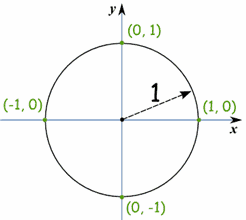
单位圆
你刚才玩的是 单位圆。
单位圆是圆心在 0,半径为 1 的圆形。
因为半径是 1, 我们可以直接在单位圆中测量正弦、余弦和正切的值。
在这里可以看到在单位圆里的正弦函数:
所以,三角法也是和 圆形有关联的!
注意:你可以看看这些美丽的正弦、余弦和正切图。
度与弧度
| 角 | 度 | 弧度 |
|---|---|---|
| 90° | π/2 | |
| __ 平角 | 180° | π |
| 360° | 2π |
重复的规律
因为角是环绕着圆周转动的,正弦、余弦和正切也每个全转重复一次 (去 振幅、周期、相移和频率 看看)。
若需要求大于一个全转,就是 360°(2π 弧度)的角的函数,便要把角度转变为小于 360°(2π 弧度):
例子:370°的余弦是多少?
370°大于 360°,所以要减去 360°
370° − 360° = 10°
cos(370°) = cos(10°) = 0.985 (保留三位小数)
若角度是负数,便要加 360°(或其倍数)。
例子:−3 弧度的正弦是多少?
−3 小于 0,所以要加 2π 弧度
−3 + 2π = −3 + 6.283…… = 3.283…… 弧度
sin(−3) = sin(3.283……) = −0.141 (保留3位小数)
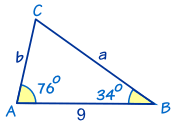
解三角形
三角法里的一个重要运算是 解三角形。 "解" 的意思是求未知的边和角。
我们也可以求未知的边长。一般规则是:
若已知任意三个边长或角度,则可求未知的三个
(除了已知三个角度的情况外)
去看 解三角形 来了解更多。
其他函数(余切、正割、余割)
和正弦、余弦和正切一样,另外还有三个以边长的商为值的 三角函数:
余割函数: |
csc(θ) = 斜边 / 对边 |
正割函数: |
sec(θ) = 斜边 / 邻边 |
余切函数: |
cot(θ) = 邻边 / 对边 |
三角法和三角形恒等式
当你对三角法有初步的了解后,你可以去学习这些:
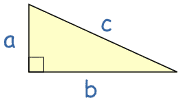 |
三角法恒等式 是对于所有直角三角形成立方程 |
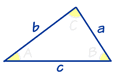 |
三角形恒等式 是对于所有三角形(不一定要是直角三角形)都成立的方程。 |
恭喜你成为三角形(和圆形)的专家!