三角法恒等式
你也许想先去看看 三角法！
直角三角形
三角法恒等式是对于直角三角形来说是成立的方程。（若不是直角三角形，你可以去 三角形恒等式 看看。）
直角三角形的每一条边都有个名字：
邻边一定实在角的旁边
对边是在角的对面
我们会学习很多不同的函数，但它们都是从一个简单的三角形衍生出来：
- 角 θ
- 斜边
- 邻边
- 对边
正弦、余弦和正切
三角法里的三个主要函数是 正弦、余弦和正切。
它们只不过是 一边的长度除以另一边的长度
对于一个直角三角形，其中一个角（不是直角）为 θ：
正弦函数： |
sin(θ) = 对边 / 斜边 |
余弦函数： |
cos(θ) = 邻边 / 斜边 |
正切函数： |
tan(θ) = 对边 / 邻边 |
以给定角度 θ，这三个比是不变的，它们的值
并不会随着三角形的大小而改变
把正弦除以余弦的结果是：
所以：
tan(θ) = sin(θ)/cos(θ)
这是第一个 三角法恒等式。
余割、正割和余切
我们也可以"反过来"除（例如 邻边/对边）：
余割函数： |
csc(θ) = 斜边 / 对边 |
正割函数： |
sec(θ) = 斜边 / 邻边 |
余切函数： |
cot(θ) = 邻边 / 对边 |
例子：若 对边 = 2，斜边 = 4，则
sin(θ) = 2/4， csc(θ) = 4/2
所以：
sin(θ) = 1/csc(θ)
cos(θ) = 1/sec(θ)
tan(θ) = 1/cot(θ)
反过来：
csc(θ) = 1/sin(θ)
sec(θ) = 1/cos(θ)
cot(θ) = 1/tan(θ)
同时：
cot(θ) = cos(θ)/sin(θ)
勾股定理
接下来我们从 勾股定理开始：
 |
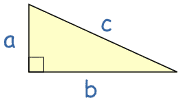勾股定理说：在直角三角形里，a的平方加b的平方等于c的平方： a2 + b2 = c2 |
除以 c2：
a2 c2 = b2 c2 = c2 c2
简化为：
( a c )2 + ( b c )2 = 1
a/c 是 对边 / 斜边，就是 sin(θ)
b/c 是 邻边 / 斜边，就是 cos(θ)
所以 (a/c)2 + (b/c)2 = 1 也可以写成：
sin2 θ + cos2 θ = 1
- sin2 θ 的意思是 θ 的正弦的平方，
- sin θ2 的意思是 θ 的平方的正弦
例子：32°
保留四位小数：
- sin(32°) = 0.5299……
- cos(32°) = 0.8480……
求 sin2 θ + cos2 θ:
0.52992 + 0.84802
= 0.2808…… + 0.7191……
= 0.9999……
只用四位小数，答案已经非常接近1。用你的计算器来试试看！
以下是一些相关的恒等式：
sin2 θ = 1 − cos2 θ
cos2 θ = 1 − sin2 θ
tan2 θ + 1 = sec2 θ
tan2 θ = sec2 θ − 1
cot2 θ + 1 = csc2 θ
cot2 θ = csc2 θ − 1
怎样去记住这么多的恒等式？以上的恒等式都可以用
|
 |
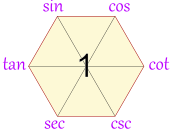慢着……还有更多！
还有很多恒等式……以下是一些比较有用的：
对角恒等式
sin(−θ) = −sin(θ)
cos(−θ) = cos(θ)
tan(−θ) = −tan(θ)
双角恒等式
 |
 |
 |
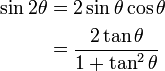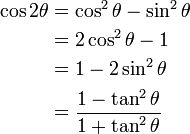半角恒等式
注意： "±" 的意思是 其中一个，视 θ/2 的值而定
 |
 |
 |
 |
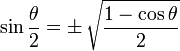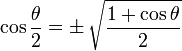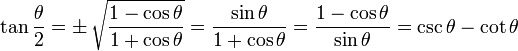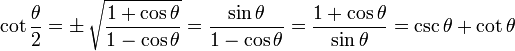角度和与角度差恒等式
注意： 
的意思是可以用加或减，
的意思是用相反的正负号。
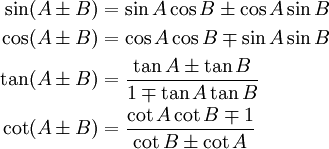
三角形恒等式
还有三角形恒等式，它们适用于所有三角形（不只是直角三角形）